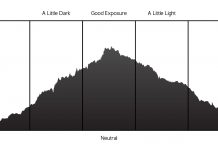
Interpolációs eljárások

Interpoláció – ezzel a szóval gyakran találkozhat a digitális fotós. Aki mélyebben beleásta magát a digitális képalkotás mikéntjeibe, az már a gépen belül lezajló folyamatoknál találkozhatott, a Bayer mozaik, színcsatornák és a lineáris interpoláció nevével. De azok is találkozhattak ezzel a folyamattal, – még ha akaratlanul is – akik legalább egy fotót nyomtattak már életükben.

Mi is az interpoláció ?

A digitális fotózásban szinte minden matematika és fizika. Az interpoláció alapvetően a matematika tudományához köthető fogalom.

Már szinte látom, ahogy az érzékenyebb lelkű olvasóknak e szavak hallatán hideg veríték ül ki tarkójukra és máris az egér után nyúlnak, hogy itt fejezzék be a cikk olvasását. Ne tegyék kedves olvasók! Ígérem, hogy nem mélyedünk bele túlságosan ezen tudományágak rejtelmeibe, csak amíg szükséges és a cikk írója is érti, amiről ír.

Az interpoláció lényegében bizonyos számú ismert értékből határoz meg egy vagy több ismeretlen értéket. A meghatározás folyamata különbözteti meg egymástól az interpolációs eljárásokat. Ez számos módon történhet.

Miért érdekel ez bennünket ?

Ahogy fentebb említettem, aki nyomtatott vagy felnagyított már fotót, az találkozhatott az interpolációval.

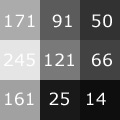
Egy digitális fotó képpontokból (pixelekből) áll. Minden egyes képpont leírható matematikai értékkel. Az egyszerűség kedvéért maradjunk egy fekete-fehér digitális fényképnél. A fotó minden egyes képpontjához egy 0 és 255 közötti számérték rendelhető. Íme egy fekete-fehér (szürkeárnyalatos) fotó részlete, felnagyított pixelekkel és a hozzájuk tartozó világossági értékkel.

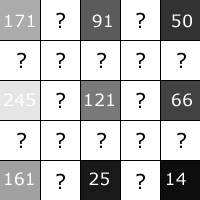
A digitális fotó nagyításakor eredeti méretének akár többszörösére is nőhet, valódi számérték azonban csak az eredeti képpontokhoz tartozik, a nagyítás során „beillesztett” új képpontok értékét hivatott kiszámolni az interpolációs algoritmus. Az előző képrészlet nagyított változatában a cél a köztes képpontok világosság értékének meghatározása. Erre szolgál az interpoláció.

A legegyszerűbb interpolációs algoritmus a Legközelebbi szomszéd, ismertebb angol nevén Nearest neighbor. Nem csinál mást, mint az ismert pixel értékét behelyettesíti az ismeretlen összes környező pixelhelyre. Így növekmény ugyanazt az értéket kapja, mint az eredeti pixel, ugyanolyan színű és világosságú lesz. Ez a leggyorsabb módszer, de egyben a legpontatlanabb is. Túlzott nagyításnál a kép kusza, széteső lesz.

Gyakorta használt eljárás a Kettős lineáris, vagyis Bilinear is. Itt a két ismert pixel közti képpontokat fokozatos lépésközökkel határozza meg a program. Egy ismert 10 és 30 értékű képpont közé például 20-as értékű képpont kerül. A Kettős lineáris interpoláció többnyire 4 környező pixel alapján számol, vízszintes és függőleges irányban. Az eredmény egy nagyítva is képszerű, de meglehetősen elmosott fotó.

Az úgynevezett Kettős köbös, azaz Bicubic interpoláció 16 környező képpontok alapján átlagol.

Hasonló módon működnek más hagyományos (pl. Bspline, Lanczos) eljárások is. A különbség a képpontokat kiszámító matematikai modell, ami látható különbségekhez vezethet.

Az interpolációs eljárások között megkülönböztetünk hagyományos (pl. Nearest neighbor, Bilinear, Bicubic, Bspline, Lanczos) és adaptív (pl. Geniune Fractal, Sspline) módszereket. A hagyományos módszerek mindig csak a környező ismert pixelek átlagát veszik a számítás alapjául, így a meghatározandó pixel értéke csupán annak képen elfoglalt pozíciójától függ. Az adaptív interpolációk viszont az egyes pixelek értékeit is figyelembe veszik

Az újfajta interpolációs eljárások nem csak a képpont értékeket, hanem a kép karakterét – az éleket, a mosott területeket – is figyelembe veszik, hogy a nagyított kép is megőrizze az eredeti méretű kép alapvető tulajdonságait. Mindezt egybevéve a következőkben megvizsgáljuk néhány interpolációs algoritmus eredményeit.

Hogyan teszteltünk?

Tizenkét fejlettebb, fejletlenebb interpolációs eljárást vettünk alapul, melyek többsége az általánosan használt képszerkesztő, vagy katalogizáló programokban megtalálható. Három szoftvert használtunk fel erre a célra.

Adobe Photoshop

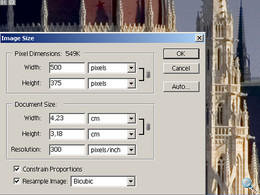Világszerte ismert és elismert fotószerkesztő alkalmazás. Képméret (Image Size) szekciójában háromféle alapvető interpolációs eljárás közül választhatunk: Nearest neighbor, Bilinear és Bicubic.

Az újabb programverziókban választható még kétféle Bicubic karakter, lágyabb és élesített végeredménnyel. A kép nagyításra a megszokott pixel és nyomtatási oldalméret, valamint felbontás beállítások használhatók.

Genuine Fractal PrintPro

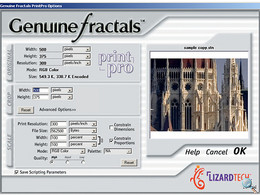A LizardTech, főként nyomtatáshoz és méretezéshez használható fraktálos pluginja, melyet a Photoshopban használtunk. Alkalmazása kissé körülményes. A nagyítandó képfájlt először a plugin saját .STN (STING) formátumába kell mentenünk , mely veszteségmentes illetve veszteséges tömörítéssel lehetséges. A mentett fájlt ezután megnyitva automatikusan megnyílik a programablak, ahol fraktálos interpolációra illetve részlet kivágásra nyílik lehetőségünk a Photoshopnál összetettebb beállításokkal, háromfokozatú minőség választással. A méretezési paraméterek külön menthetők.

XnView

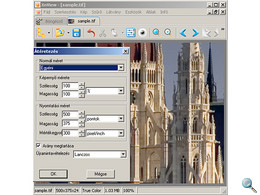Ingyenes képkatalogizáló alkalmazás, kiterjedt képszerkesztési funkciókkal. Méretezési lehetőségei nagyjából a Photoshoppal azonosak, azzal különbséggel, hogy 8 féle interpolációs eljárást választhatunk. Az ott megismert Nearest neighbor és Bilinear módozatokon túl a Hermite, Gaussian, Bell, Bspline, Mitchell és Lanczos metódusokat használtuk.

Photozoom Professional

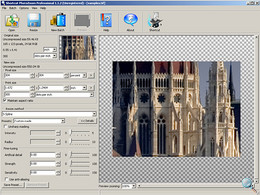Az egykori S-spline Pro szoftver továbbfejlesztett utódja, a Shortcut cég gondozásában. Méretezéshez használható célszoftver, így nem meglepő, hogy ez a szoftver nyújtja a legtöbb szolgáltatást ezen a téren. Alapvetően a Sspline interpolációra épül, de további 9 interpolációs eljárás választható. Előre mentett minőségi beállításokat, élesítést, a képkarakter finomhangolását és élsimítást is alkalmazhatunk segítségével.

Kissé kakukktojás jellegű volt a lépcsős (Stair) interpoláció néven elhíresült metódus alkalmazása. Több plugin és Photoshop action is használja ezt a módszert (pl. Fred Miranda’s Stair Interpolation). Lényege, hogy nem egy lépésben, hanem több, finom ugrással méretezünk föl egy képet, így jobb eredményt kapva. A módszert a Photoshop Bicubic interpolációjának 110%-os lépéseivel alkalmaztuk.

A felhasznált interpolációk tehát:

• Nearest neighbor
• Bilinear
• Bicubic
• Hermite
• Gaussian
• Bell
• Bspline
• Mitchell
• Lanczos
• Sspline
• Genuine Fractal
• Stair (Bicubic)

Így állt össze a „piszkos tizenkettő”, akiket kétféle eljárással próbáltunk kellemetlen helyzetbe hozni. Egy Adobe RAW konverterrel 8 bites TIFF formátummá alakított, Canon RAW (CRW) fotóból kivágtunk egy 500×375 képpontot részletet. A kép előzetesen élesített volt. A részletet először az adott interpolációs eljárással 33%-ra kicsinyítettük, majd ugyanazzal az interpolációs technikával ismét 500×375 képpont nagyságúra növeltük, így megkaptuk az eredeti méretet.

A másik módszerrel egy 100×100 képpontos, vektoros formákból és text elemekből álló bitmap képet 500%-ra nagyítottunk.

Eredmények

	Összehasonlításként a két eredeti kép. Kattintson a nézőképekre az eredeti méret megtekintéséhez!

Nearest neighbor

A végeredmény sejthető volt. A legegyszerűbb interpolációs algoritmus a legközelebbi ismert pixelek értékeit alkalmazta a növelt kép ismeretlen pixeleinek kiszámításához. A kapott fotó részletei elnagyoltak szétesők. Bár a fotórészlet több helyen is az élesség látszatát kelti, de ez nem a valós élek, hanem a nagymértékben eltérő értékű pixelek határán kialakult kontrasztkülönbség. Az algoritmus alkalmazása legfeljebb apró nagyításoknál indokolt, megfeledkeznünk azonban mégsem kell róla. Kitűnően használható, bizonyos képhibák, vagy fontos képrészletek pixelszintű prezentációjánál, mondjuk színhiba, halo jelenség mérésénél.

Bilinear

Kicsinyített majd felnagyított képrészletünk szépen megtartotta a karakterét, a formák felismerhetőek, bár a haránt futó éleknél enyhe lépcsősség tapasztalható. A részletesség, figyelembe véve az eljárás egyszerűségét, meglepően jó. Az egész kép jól jellemezhetően lágy, mosott, fátyolos hatást kelt. A kép utólag jó hatásfokkal élesíthető, de az ívelt formák és ferde élek struktúrája szétesik. Az ábrás tesztnél még jobban tetten érhető az élek lépcsőzetessége és a relatív részletnélküliség. A formák azonban jól felismerhetően kevéssé torzultak.

Bicubic

Az előzőnél határozottabb karakter jellemzi a képet. A fátyolosság eltűnt, az élkontraszt magas, kissé túlzó. A részletesség a nagyobb kontraszt miatt láthatóan nőtt, de képi világ kissé „zaklatottab”, irreálisabb, több esetben hamis formák, élek alakultak ki. Bár a bilineárisnál jobb eredményt kapunk az élsimítás terén, maradéktalanul itt sem tudott megbirkózni a feladattal az interpoláció. A második képen jól látni az élsimítás kedvezőbb hatását, a jobb kontrasztot és élességet.

Hermite

	A végeredmény mintha a Bicubic és a Nearest neighbor interpoláció ötvözete lenne. A részletesség meglehetősen jó, a sima felületeken nem nőtt a zaj. A formák azonban kissé elnagyoltak és a kontraszt is kisebb. Az ívek és élek simítása gyenge. Ugyanez jellemző a nagyított, ábrás képre is, ahol még szembetűnőbbek a lépcsőzetes, elnagyolt formák.

Gaussian

	A bilineáris interpolációnál tapasztalt fátyol újra visszatért, ezúttal hatványozottan. A kép még lágyabb hatást kelt, alacsony részletesség és kontraszt mellett. Az élsimítás sokkal hatásosabb az eddigieknél. Az ábrás képen jól megfigyelhetőek a homályba vesző formák.

Bell

	Hasonló eredményt kaptunk, mint a Gaussian interpolációnál, de jobban megfigyelve a képet, mind a kontraszt, mind a részletesség leheletnyit romlott. Az élsimítás egy fokkal javult, ami különösen a második kép meredekebb, ferde éleinél látható, és közelít a nagyon jóhoz. Sajnos a kép életlensége ront az összhatáson.

Bspline

Idei homály versenyünk győztese. Jól láthatóan életlenebb, elnagyoltabb formák, mint bármelyik más interpolációnál. Alkalmazása erősen zajos, vagy lágy átmeneteket és kevés részletet tartalmazó képeknél ajánlott. Irreális részletet nem találunk a fotókon, minden egy kellemes, langyos zselé alatt pihen. Az élsimítás itt a legjobb, bár ilyen lágyságnál nem hiszem, hogy komolyabb lépcsőzetességről egyáltalán szót ejthetnénk.

Mitchell

Mind kontraszt, mind élesség tekintetében a Bilineáris algoritmussal mutat rokonságot. A képrészletesség is hasonló, bizonyos területeken az egyik, más helyeken a másik mutat jobb részletességet. Egyben a Gaussian, Bell és Bspline metódusoknál jobb végeredményt mutat ezeken a területeken. A ferde élek kezelésében túllép a Bilineáris interpoláción. A második képen jól látszik, hogy ilyen téren a Gaussian módszerrel rokonítható, annál jobb kontraszttal és élességgel.

Lanczos

A magyar származású matematikus, Lánczos Kornél nevéhez fűződő interpolációs algoritmus az eddigi leghatározottabb élkontrasztot és részletességet hozza, hasonlóan a Bicubic eljáráshoz, de annál egy fokkal erőteljesebben. A két metódus sok tekintetben mutat hasonlóságot egymáshoz. Sok részletet tartalmazó képek nagyításához kétségtelenül mindkettő jól használható. A második képen megfigyelhető, hogy a határozottabb élesítés egyfajta „aurát” alakított ki a képelemek körül, ami simább felületeknél zavaró is lehet.

Genuine Fractal

Kiváló élesség, de nem túl meggyőző részletesség jellemzi, mérsékelt, jól adagolt, nem túl tolakodó kontraszt mellett. Az eddig vizsgált interpolációk közül határozottan a legjobb eredményt nyújtaná, ha nem társulna ezzel a részletek magas fokú irrealitása, természetellenessége. Zaklatott, mozgalmas, Van Gogh ecsetvonásait idéző, festményszerű élményt nyújt. A második képen jól látható, hogy milyen jól megbirkózik a haránt élekkel, legyenek azok meredeken vagy enyhén futók. Az egyszerűbb ívelt formák sem okoznak neki gondot. Az összetettebb, kisebb részleteknél azonban az előzőekhez hasonló határozottsággal jár el, így a végeredmény több esetben természetellenes alakzat.

Sspline

A fraktálos interpolációnál nagyobb – kissé túlzó – kontrasztot mutat, hasonlóan kiváló élesség mellett, jobb részletességgel. Élsimítás terén kicsit az előbbi alatt marad, de így is nagyon jó eredményt produkál. Az Spline-nak szintén meggyűlt a baja a formák hű visszaadásával. Nagyfokú irrealitás jellemzi a fotórészletet, ezúttal is impresszionista festményre hasonlító karakterrel, de inkább Monet-ra hasonlító „ecsetkezeléssel”. A formák összességében jobban tükrözik a valóságot, mint a Fractal interpoláció esetében. Ez jól megfigyelhető a második kép finomabb részleteinél, ahol határozottan jobban vizsgázott az Sspline. A fraktálos interpoláció előnye az elkeskenyedő formák rajzában van, iit az Sspline nagyvonalúbb, de az többi algoritmusnál pontosabb. Az Sspline előnyének hozhatjuk fel a Photozoom program nyújtotta széleskörű beállítási lehetőségeket. Példánkban nem alkalmaztunk külön élesítést az interpolációhoz, hiszen a többi algoritmus is ily pőrén szerepelt, de a program lehetőséget nyújt az Sspline interpoláció élességének meghatározásához is, valamint lehetőség van a karakter finomhangolására, többek között műrészletek képbe vegyítésével és jobb élsimítással.

Stair (Bicubic)

A Photoshop program képnagyítás szekciójában, egyszerű Bicubic interpolációval, de több lépésben kicsinyítettük és nagyítottuk a képeket. 90%-os kicsinyítési lépéseket és 110%-os nagyításokat használtunk. A módszer jobb eredményt ad, ha 3-4 lépcsőnként enyhébb élesítést is alkalmazunk a képre. Az enélkül kapott eredmény látható balra, mely a hagyományos Bicubic interpolációnál erősebb kontrasztot mutat, elnagyolt formákkal és rosszabb részletességgel, és élességgel, viszont a jobbak közé sorolható élsimítással. Összességében a kép karaktere nem kelt a szemlélőben kellemes benyomást. Valószínűleg a lépcsőzetesen méretcsökkentett, majd nagyított kép, kissé túlzás ezen algoritmus számára. Kizárólag kicsinyítésre vagy nagyításra használva pontosabb eredményt kapunk. Bizonyítja ezt az is, hogy a második, csak nagyított képnél is jól látszanak a nagyvonalúan kezelt, mosott formák, de a sokkal jobb élsimítás is. Itt összességében nincs hiányérzetünk, az amúgy jól teljesítő Bicubic interpolációhoz képest.

Összegzés

A tapasztaltak alapján elmondható, hogy a legegyszerűbb interpolációs algoritmusok közül megfelelő eredmény érhető el már a Bicubic metódus alkalmazásával is, hiszen egyáltalán nem marad el az „egzotikusabb” eljárások mögött. A hagyományos, ingyenesen is beszerezhető eljárások között a Lanczos interpolációval kapunk a Bicubichoz sok tekintetben hasonló, némely téren azonban jobb eredményt.

A piszkos tizenkettő legjobbjai a végeredményt tekintve a G Fractal és az Sspline interpolációk, szolgáltatások terén pedig a széleskörűen hangolható Sspline viszi el a pálmát, amely ezzel együtt harci feladatunk abszolút túlélőjének bizonyult. A kiváló Photozoom Professional program képfinomító szolgáltatásaival karöltve több tartalék rejlik ebben az algoritmusban, mint a többiben. Hátránya, hogy ez az algoritmus ingyenes szoftverben nem elérhető.