(A sorozat korábban a szerző saját weboldalán volt olvasható.)
Az optikában, a fizika más területeihez hasonlóan egyszerűsített modelleket alkalmaznak a jelenségek tanulmányozásához. A legfontosabb fogalmak megértéséhez ezért nem veszünk figyelembe minden tényezőt. Mint ismert, két különböző törésmutatójú anyag (pl. levegő-üveg) határán a fény egy része behatol az anyagba és megváltoztatja irányát (fénytörés), míg másik része visszaverődik vagy elnyelődik. Számunkra a behatoló fénysugarak a fontosabbak, ezért most csak ezekkel fogunk foglalkozni. Szintén a könnyebb érthetőség kedvéért az ebben az írásban szereplő távolságadatokat, méreteket előjel nélkül alkalmazzuk.
A lencse
A fényképező objektív optikai elemek (lencsék vagy tükrök) olyan együttese, amely a megörökíteni kívánt tárgyról vagy tárgyakról a fényképezőgép fényérzékeny felületére (film vagy képérzékelő) vetít képet. Az objektívekben leggyakrabban használt optikai elem a lencse. A lencséket általában két gömbfelület határolja, és átlátszó anyagból készülnek (optikai üveg). A felületeket meghatározó gömbök középpontjait összekötő egyenes a lencse tengelye. A gyűjtőlencsék esetében a tengely mentén mért vastagság nagyobb, mint a széleken. A szórólencsék széleiken vastagabbak, mint tengelyüknél. A legegyszerűbben tárgyalható lencsetípus a kétszer domború (bikonvex) lencse, ezért a lencsék alapvető viselkedését, ami a fényképezés szempontjából is a legfontosabb jelentőséggel bír, ezzel fogjuk megvizsgálni.
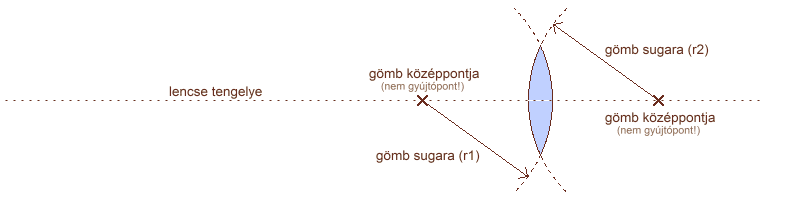
kétszer domború gyűjtőlencse tengelye és gömbfelületei
Gyújtótávolság, fősíkok
A saját fénnyel rendelkező vagy a megvilágított és fényt visszaverő tárgyak felületét fénysugarak hagyják el. Ha a tárgy a lencse tengelyén, végtelenül messze van, akkor a fénysugarak egymással és a tengellyel párhuzamosan fogják a lencse felületét elérni. Ilyenkor a gyűjtőlencse a tárggyal ellenkező oldalon egy pontba fókuszálja a fénysugarakat. Ezt a nevezetes pontot a lencse gyújtópontjának nevezik. Ha a lencsébe behatoló és a lencsét elhagyó fénysugarakat meghosszabbítjuk a lencse belseje felé, az egyenesek metszeni fogják egymást. Több fénysugárra megismételve a műveletet a metszéspontok egy síkot jelölnek ki. Ezt nevezzük a lencse fősíkjának. A fősíkok nagymértékben leegyszerűsítik a fény útjának számítását, hiszen úgy működnek, mintha csak egy helyen törne meg a fény, miközben a valóságban a lencsébe való be- és kilépéskor is fénytörés következik be. A két oldalról érkező fénysugarak két különböző fősíkot jelölnek ki. Ha a lencse átmérője sokkal nagyobb, mint a vastagsága, akkor ezek a fősíkok elhanyagolhatóan közel kerülnek egymáshoz, így nem okoz komoly számítási hibát, ha csak egy fősíkkal számolunk. Az ilyen lencsét az optikában vékony lencsének nevezik. Ahol a fősíkot a tengely átdöfi, ott a lencse főpontja.
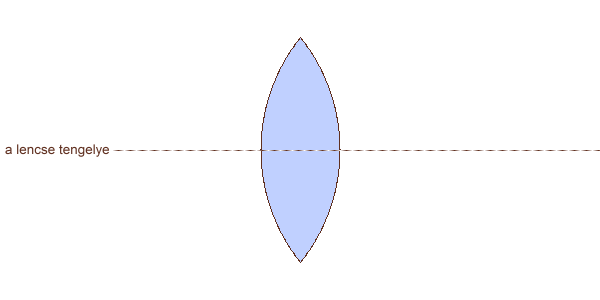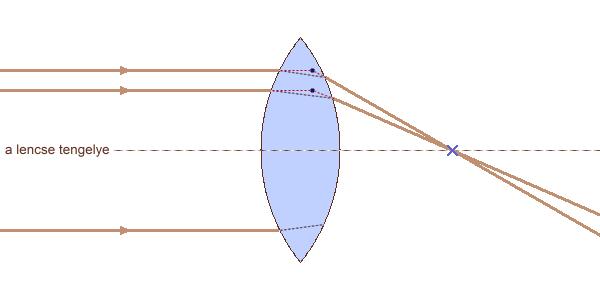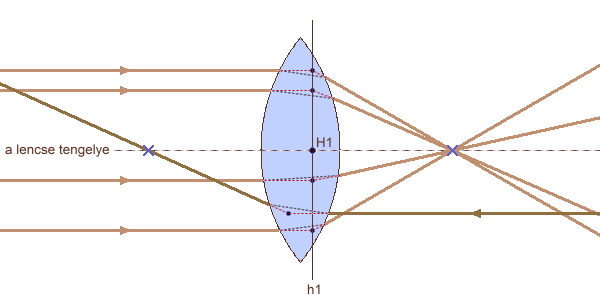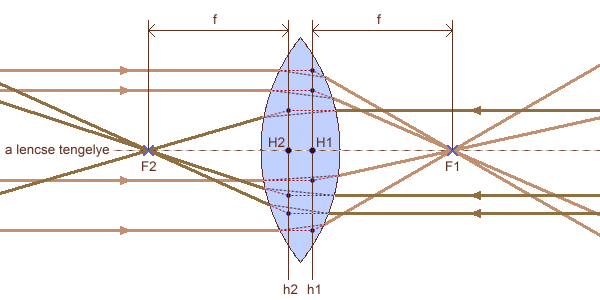
fénysugarak haladási iránya végtelenül messze lévő fényforrás esetén
h1,h2: fősíkok H1,H2: főpontok F1,F2: gyújtópontok f: gyújtótávolság
Ha a fényforrást a gyújtópontba helyezzük, akkor a gyűjtőlencse túloldalán a tengellyel párhuzamos fénysugarak jelennek meg. Fontos észrevenni, hogy míg az előző esetben a fény behatolási pontjához képest távolabb eső fősík határozza meg a fénysugár látszólagos törésének helyét, ebben az esetben a közelebb eső fősík teszi ezt meg. Ennek a vastag lencsék vizsgálatánál lesz jelentősége.
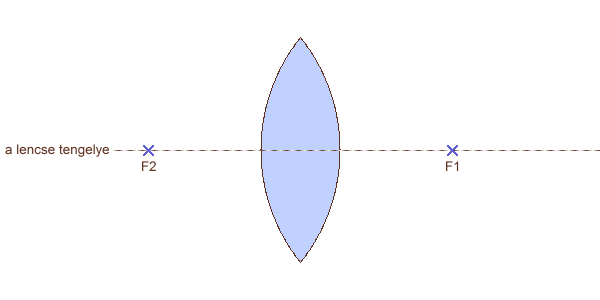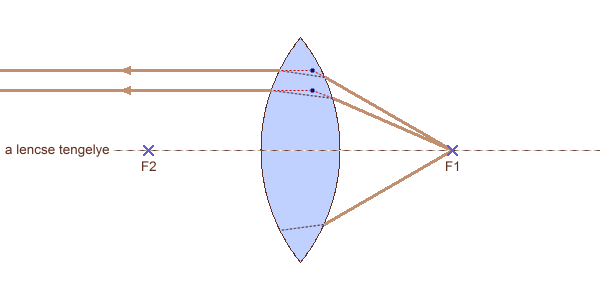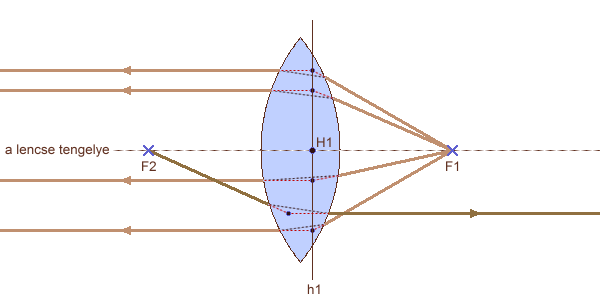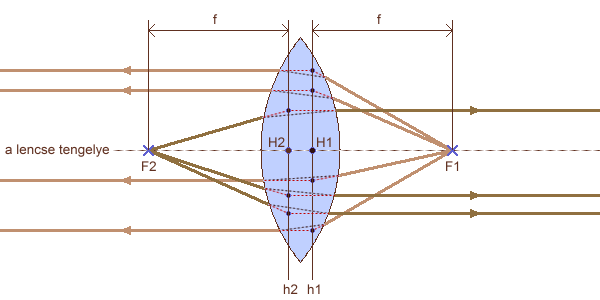
fénysugarak haladási iránya a gyújtópontban lévő pontszerű fényforrás esetén
h1,h2: fősíkok H1,H2: főpontok F1,F2: gyújtópontok f: gyújtótávolság
A gyújtópont távolsága a fősíktól a lencse gyújtótávolsága (f). A méterben kifejezett gyújtótávolság reciprok értéke a dioptria (d = 1/f). Ha a tárgyat közelítjük a lencse felé, már nem lesznek párhuzamosak a fénysugarak, ezért a lencse saját gyújtópontja mögé fog fókuszálni. Minél közelebb kerül a tárgy a lencséhez, annál távolabb kerül a fókuszálás pontja. Ha a tárgy fősíktól mért távolsága megegyezik a gyújtótávolság kétszeresével, a fénysugarak a lencse mögött is pont ilyen távolságra fogják egymást metszeni. A gyújtótávolság definíciójaként szolgáló két helyzetből (a lencse a végtelenből érkező fénysugarakat egy pontba gyűjti, a gyújtópontig közelített fényforrásból indulókat pedig párhuzamosítja) már sejthető egy újabb is: a gyújtópontnál is közelebbről induló fénysugarak a túloldalon széttartóak lesznek. E jelenségek magyarázatát a lencse leképzési törvényében kell keresni.
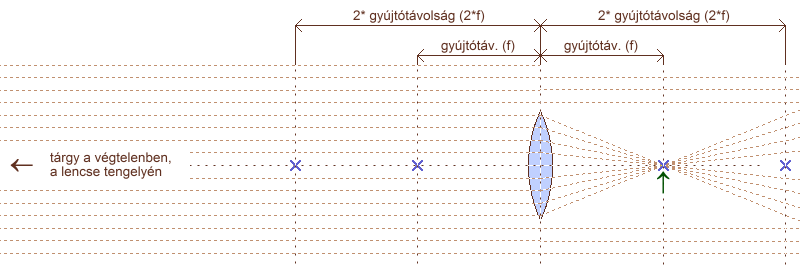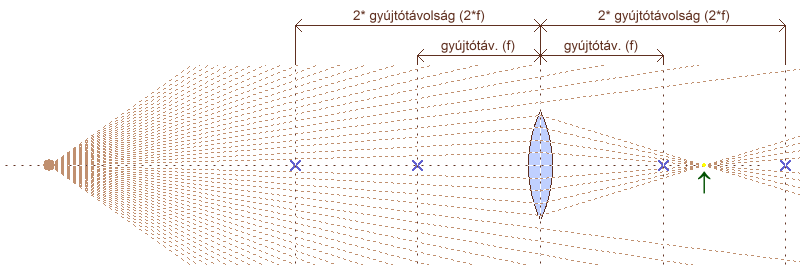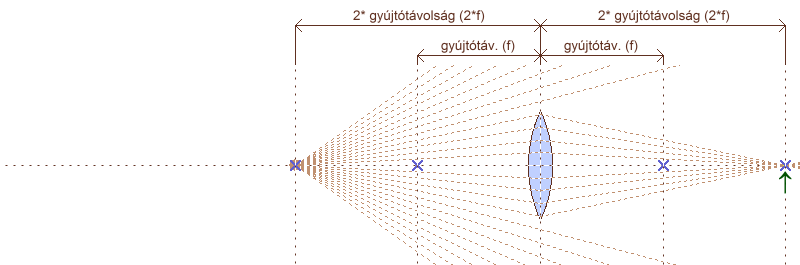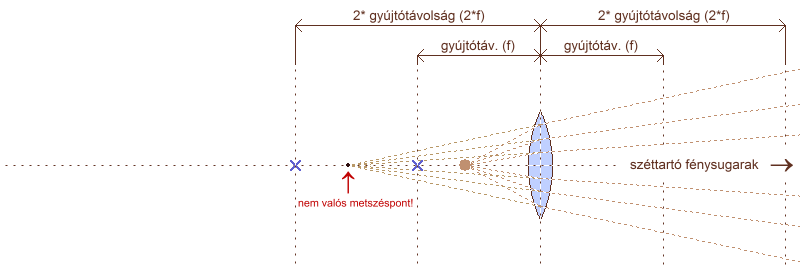
közeledő, pontszerű fényforrás hatása (vékony lencse – egy fősík)
A leképzési törvény
A nagy kiterjedésű tárgyakról érkező fény felfogható úgy, mint pontszerű fényforrások összessége. A lencsék viselkedésének tanulmányozására használt optikai modellben ezek a pontszerű fényforrások a tárgypontok. A tárgypont a tárgysíkon helyezkedik el, amely párhuzamos a lencse fősíkjával és merőleges a tengelyére. A tárgypontból induló fénysugarakat a gyűjtőlencse egy pontba fókuszálja, ezt nevezik képpontnak, az általa meghatározott, fősíkkal ugyancsak párhuzamos síkot pedig képsíknak. A tárgysík és a lencse fősíkjának távolsága a tárgytávolság (t), a képsík és a fősík távolsága a képtávolság (k). A leképzés nem más, mint a tárgypontokhoz a megfelelő képpontok hozzárendelése, azaz annak meghatározása, hogy a lencse fősíkjához és tengelyéhez mérve bárhol elhelyezkedő tárgyból kiinduló fénysugarakat a lencse hová fogja fókuszálni. Ehhez találnunk kell két különböző, egymást metsző fénysugarat, amelynek útját meg tudjuk mondani az eddig ismert törvények alapján. A következő, karakterisztikusnak is nevezett két fénysugár megfelel ezeknek a feltételeknek:
- a tárgyoldali gyújtóponton áthaladó fénysugár a tengellyel párhuzamosan hagyja el a lencsét, miután a fősíkon megtört
(az ábrán szaggatott, zöld színű vonallal jelölve) - a lencse tengelyével párhuzamos fénysugár a fősíkon való megtörés után át fog haladni a képoldali gyújtóponton
(az ábrán szaggatott, cián színű vonallal jelölve)
Ez utóbbi fénysugár a lencse előtt kijelöli a tárgyvonalat, mögötte pedig a képvonalat. A tárgypont tengelytől mért távolsága a tárgynagyság (T), a képpont tengelytől mért távolsága a képnagyság (K).
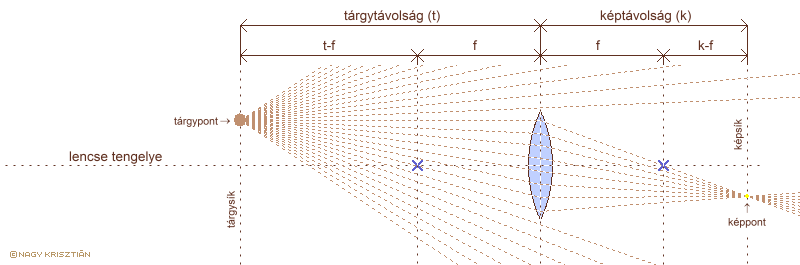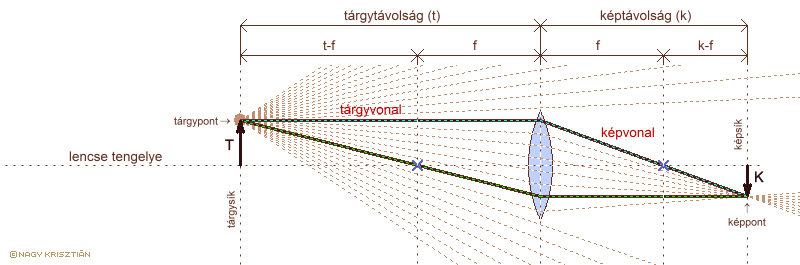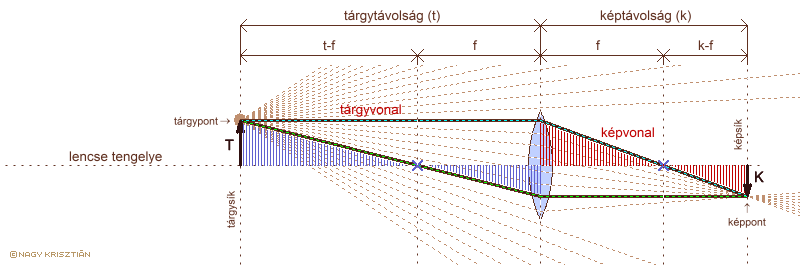
a leképzési törvény levezetése vékony lencsére
T: tárgynagyság K: képnagyság t: tárgytávolság k: képtávolság
Az ábrán a szemléletesség kedvéért a tárgynagyság kisebb, mint a lencse átmérőjének fele, hogy a tárgyvonal áthaladjon a lencsén. A szerkesztés azonban ugyanígy elvégezhető akkor is, ha a tárgynagyság sokkal nagyobb, ezért a tárgyvonal nem a lencsében metszi a fősíkot. A színekkel jelölt háromszögek páronként hasonlóak, mert:
– páronként van egy-egy csúcsszögük
– mind a négy derékszögű háromszög
|
K / T = ( k – f ) / f |
a pirossal jelölt háromszögek alapján felírható aránypár |
|
K / T = f / ( t – f ) |
a kékkel jelölt háromszögek alapján felírható aránypár |
|
( k – f ) / f = f / ( t – f ) |
a bal oldalak egyenlőek, ezért a jobb oldalak is |
|
( k – f )( t – f ) = f 2 |
szorozva f * ( t – f ) -fel (ez Newton képlete) |
|
kt – kf – tf + f 2 = f 2 |
bal oldalon a szorzást elvégezve |
|
kt = kf + tf |
f 2 -t mindkét oldalból kivonva és átrendezve az egyenletet |
|
1 / f = 1 / t + 1 / k |
osztva fkt -vel megkapjuk a leképzési törvényt |
A (k-f) és (t-f) méreteket nevezik gyújtóponttól számított vagy Newton féle tárgy- és képtávolságnak is. Most fejezzük ki a képtávolság és a tárgytávolság arányát:
|
K / T = ( k – f ) / f |
először újra a pirossal jelölt háromszögek alapján felírható aránypár |
|
Kf / T = k – f |
f -fel szorozva |
|
Kf / T + f = k |
f -t a másik oldalra |
|
( Kf + Tf ) / T = k |
a bal oldalt közös nevezőre hozva megkaptuk a k -t |
|
K / T = f / ( t – f ) |
majd újra a kékkel jelölt háromszögek alapján felírható aránypár |
|
T / K = ( t – f ) / f |
mindkét oldal reciprok értéke |
|
Tf / K = t – f |
f -fel szorozva |
|
Tf / K + f = t |
f -t a másik oldalra |
|
( Tf + Kf ) / K = t |
a bal oldalt közös nevezőre hozva megkaptuk a t -t |
|
|
|
|
( Kf + Tf ) / T |
|
|
k / t = ────────── |
osszuk el az imént kifejtett k-t a t -vel |
|
( Tf + Kf ) / K |
|
|
|
|
|
k / t = K / T |
egyszerűsítve ( Kf + Tf ) -vel |
Ez azt jelenti, hogy a kép- és a tárgytávolság aránya egyenlő a kép- és a tárgynagyság arányával. Fordítsuk meg a bizonyítás irányát, algebrai formából haladjunk a geometriai felé. Ha a főpontot összekötjük mind a tárgyponttal, mind a képponttal, az így keletkező (az ábrán zöld színnel jelölt) háromszögek hasonlóak, hiszen derékszögűek, és oldalaikról tudjuk, hogy K / T = k / t teljesül. Ezekből következik, hogy a főpontnál lévő szög csúcsszög, a két egyenes egybeesik, tehát a tárgypontot a képponttal összekötő egyenes átmegy a főponton. Másképpen fogalmazva: vékony lencse esetén a tárgypontból kiinduló, főponton áthaladó fénysugár irányváltoztatás nélkül hagyja el a lencsét.
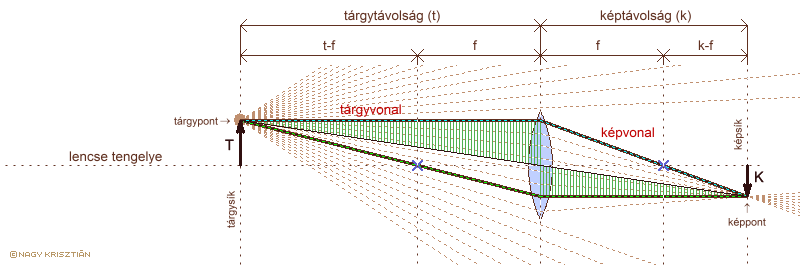
A K / T = k / t egyenlet és a főponton áthaladó fénysugár összefüggése
A K/T = N hányados neve: oldalnagyítás vagy lineáris nagyítás. A tárgysíkban elhelyezkedő (kétdimenziós) tárgy méretét N értékével szorozva megkapjuk, mekkora lesz a képsíkban a tárgy vetülete. Most nézzük meg, milyen hatásssal van a tárgy- és képtávolságra, ha az oldalnagyítás 1-szeres:
|
K / T = N = 1 |
az oldalnagyítás 1-szeres |
|
1 = f / ( t – f) |
a K / T hányadost beírva a levezetés második aránypárjába |
|
t – f = f |
mindkét oldalt ( t – f ) -fel szorozva |
|
t = 2f |
átrendezve az egyenletet |
|
k = 2f |
ha az első aránypárból vezetjük le, erre jutunk |
|
k = t |
a két utóbbi egyenletből következik |
Tehát akkor egyenlő a tárgynagyság a képnagysággal, azaz akkor 1-szeres az oldalnagyítás, ha a tárgytávolság és a képtávolság a gyújtótávolság 2-szerese. A lineáris nagyítást gyakran nem hányadosként, hanem az arány megadásával fejezik ki, képnagyság : tárgynagyság formában, a kisebbet 1-re normalizálva. (pl. 1:4 megfelel 0,25-szörös, 2:1 pedig megfelel 2-szeres oldalnagyításnak) Még egy különleges esetet érdemes megvizsgálni, amikor a tárgytávolság kisebb a gyújtótávolságnál:
|
t < f |
ha a tárgytávolság kisebb a gyújtótávolságnál |
|
1 / t > 1 / f |
akkor a reciprok értékeikre a fordítottja igaz |
|
1 / f = 1 / t + 1 / k |
az eredeti leképzési egyenlet |
|
1 / f – 1 / t = 1 / k |
átrendezve az egyenletet |
|
1 / f – 1 / t < 0 |
a kisebb számból egy nagyobbat kivonva negatív számot kapunk |
|
1 / k < 0 |
ami így az egyenlet másik oldalára is igaz |
|
k < 0 |
ez pedig csak úgy lehetséges, ha k negatív |
Tehát ebben az esetben a képtávolságra negatív érték jön ki, nem keletkezik hagyományos értelemben vett kép. A képoldalon a széttartó fénysugarakat a tárgyoldal felé meghosszabbítva kapunk csak metszéspontot. Ez azonban nem valós kép, hanem virtuális. Ha t = f, tehát a tárgy a gyújtópontban van, a képtávolságra az egyenlet alapján végtelen nagy érték jön ki, a megtört fénysugarak párhuzamosak lesznek, azaz visszajutottunk a gyűjtőlencse eredeti definíciójához.
A vastag lencse
Mint ahogyan már említettük, a valódi lencsék két fősíkkal rendelkeznek. Ha a lencse vastagsága nem elhanyagolható az átmérőjéhez képest, akkor a két fősík közötti távolsággal is számolni kell. Ezt a modellt nevezik vastag lencsének. Tanulmányozásukhoz szerencsére nem kell mást tennünk, csak a két fősíkot elnevezni és a tárgytávolság, gyújtótávolság fogalmakat újra definiálni. Ezek után a leképzési törvény és a nagyítás számítása pontosan ugyanúgy alkalmazható, mint vékony lencse esetén. Míg a vékony lencsénél a karakterisztikus sugarak által alkotott trapéz csúcsai közül kettő az egyetlen fősíkon van, itt az egyik csúcs az egyik, a másik csúcs a másik fősíkra esik. Ezen a ponton van jelentősége a gyújtópont magyarázatánál tárgyaltaknak. Ha a fénysugár a tengellyel párhuzamosan érkezik, akkor a lencsébe lépéstől távolabb eső fősík a meghatározó, ha a gyújtópont felől érkezik, akkor a közelebb eső fősík.
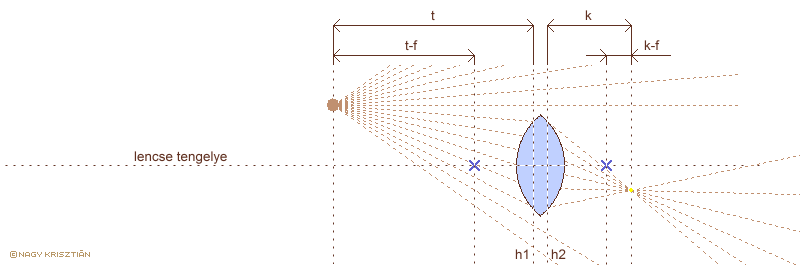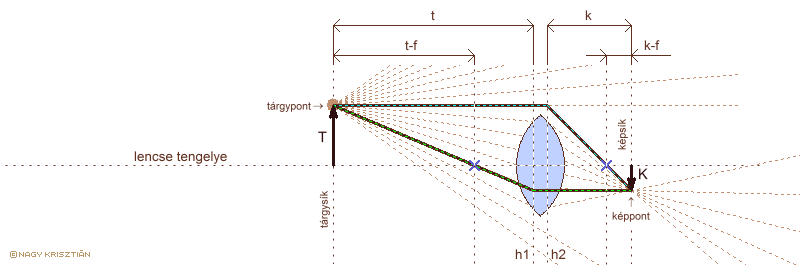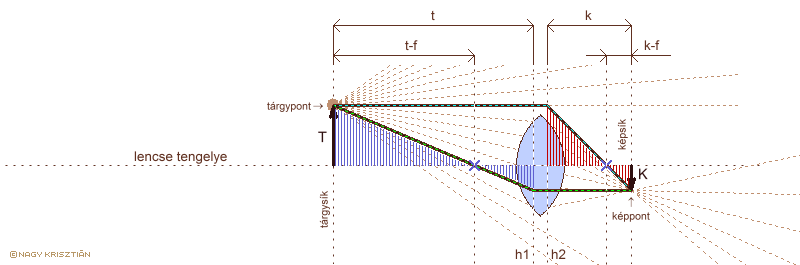
a leképzési törvény levezetése vastag lencsére
h1: tárgyoldali fősík h2: képoldali fősík
T: tárgynagyság K: képnagyság t: tárgytávolság k: képtávolság
Az 1 / f = 1 / t + 1 / k leképzési egyenlet ugyanúgy levezethető, mint előzőleg. Az alapfogalmakat a következőképpen lehet meghatározni:
|
tárgyoldali fősík |
a tárgy felé eső fősík (elsődleges fősík) |
|
képoldali fősík |
a kép felé eső fősík (másodlagos fősík) |
|
tárgytávolság |
a tárgysík és a tárgyoldali fősík távolsága |
|
képtávolság |
a képsík és a képoldali fősík távolsága |
A vastag lencse modellje azért fontos, mert a valóságban a fényképezőgépek objektívjeiben mindig több lencsét alkalmaznak. Az ilyen lencserendszerek a vastag lencsékhez hasonlóan viselkednek, tehát van egy eredő gyújtótávolságuk, valamint egy eredő tárgy- és képoldali fősíkjuk. Az így meghatározott jellemzők alapján pedig a tárgy és képtávolság definiálhatóvá, a leképzés és a nagyítás számíthatóvá válik lencserendszerek esetén is.









