(A sorozat korábban a szerző saját weboldalán volt olvasható.)
Élességállítás
A leképzési törvény alapján már tudjuk, hogy a fényképezőgéppel megörökítendő tárgyak pontjait jelképező tárgypontok mindegyikéhez tartozik egy képpont, valahol az objektív mögött. Az éles kép feltétele, hogy a pontszerű tárgyról pontszerű kép keletkezzen a fényképen, ezért a fényérzékeny felületet olyan távol kell elhelyezni a fősíktól, mint az élesen látni kívánt tárgyhoz tartozó képtávolság. Nyilvánvaló, hogy így csak egy adott távolságra lévő tárgyakról fog tökéletesen éles képet alkotni az objektív. Az élességállítás az a folyamat, amely meghatározza, hogy milyen távolságra lévő tárgypontok legyenek élesek a fényképen. A fősík és a fényérzékeny felület (érzékelő) távolsága a kihuzat.

az élességállítás folyamata
Ha visszagondolunk a vastag lencsék leképzésére, belátható, hogy lencserendszerrel (összetett objektívvel) is ugyanígy zajlik az élességállítás. A kihuzatot ilyenkor a képoldali fősík és a fényérzékeny felület távolságaként definiáljuk. Az objektívek élességállító mechanizmusa tehát úgy működik, hogy a fősíkot eltávolítja vagy közelebb viszi az érzékelőhöz, ami a kihuzat növelését vagy csökkentését jeleni. Ez többféleképpen megtehető:
- az összes lencse egyszerre való mozgatásával
- a lencsék közötti távolság módosításával úgy, hogy az eredő képoldali fősík mozduljon el
Utóbbit, ha csak a belső lencsék mozognak, belső élességállításnak hívják (internal focusing – IF). Az objektív mechanikai kialakítása meghatározza, hogy a kihuzat milyen keretek között változtatható. Végtelenre állított objektív esetén a gyújtótávolság egyenlő a kihuzattal. Mivel néhány speciális esetet kivéve majd minden objektívvel lehetséges végtelenben lévő tárgyakat élesre állítani, az objektív minimális kihuzata nem lehet nagyobb a saját gyújtótávolságánál. A legnagyobb kihuzat, amely kihat arra, hogy mennyire közeli tárgyra lehet élesre állítani az objektívet, típusonként változik. Az 1:1 oldalnagyítást elérő makro-objektíveknél a legnagyobb kihuzat kétszeres gyújtótávolsággal egyenlő. A tárgysík és az érzékelő síkja közötti teljes távolságot élességállítási távolságnak nevezik. Ennek legkisebb értékét megadják az objektív adatlapján (minimum focusing distance), amely így meghatározza az objektívvel kiegészítők nélkül elérhető legnagyobb nagyítást (maximum magnification) is.
Cserélhető objektíves fényképezőgép esetén a kihuzatot külső eszközzel, közgyűrűvel vagy harmonika-kihuzattal meg lehet növelni, amelyet az objektív és a fényképezőgép közé kell elhelyezni. Ezáltal csökken a legkisebb élességállítási távolság, és növekszik az elérhető legnagyobb nagyítás. Meg kell jegyezni, hogy a nem nagy nagyításra tervezett objektívekkel gyakran komoly minőségromlás tapasztalható ilyen helyzetben. Az objektív konstrukcióját optimalizálják bizonyos nagyításokra, és nem biztos, hogy pl. makrofényképezésre megfelel egy közgyűrűvel kiegészített általános célú objektív. A korszerű objektívek úgy változtatják a kihuzat nagyságát, hogy közben több lencsetag is elmozdul különböző mértékben, ezáltal korrigálva a képalkotási hibákat. Az ilyen megoldást lebegőtagosnak (floating mechanism) nevezik.
Gyakori hiba az élességállítás fogalomköréhez kapcsolódó távolságadatok összekeverése. Kis tárgytávolság esetén ez akár több 100%-os számítási hibákhoz vezethet pl. a nagyítás, vagy az élességi viszonyok terén.
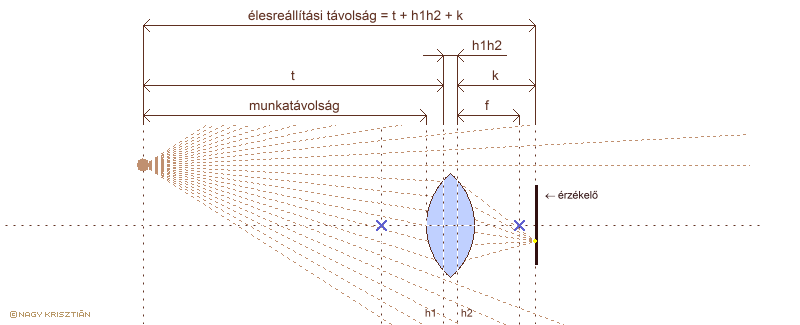
|
tárgytávolság (t), képtávolság (k) |
ezek továbbra is a tárgypont (vagy a tárgysík) és képpont (vagy a képsík) távolsága a hozzájuk közelebb eső fősíktól |
|
élességállítási távolság |
az érzékelő és az élesre állított tárgy távolsága, tehát három távolságadatból adódik össze: tárgytávolság + a két fősík egymástól való távolsága + a képtávolság |
|
munkatávolság |
alapvetően nem optikai adat, inkább mechanikai, az élesre állított tárgy és az objektív első lencséjének vagy egyéb kiálló alkatrészének távolsága |
Cserélhető objektíves fényképezőgépeken mindig megjelölik az érzékelő síkját a készülék házán egy áthúzott körrel. Innen kell mérni az élességállítási távolságot. A munkatávolság (working distance) szerepe inkább abban van, hogy pl. makrofényképezésnél akadályozza-e a fénykép elkészítését az objektív fizikai mérete. Egyszerűsége miatt kompakt kameráknál inkább a munkatávolság minimumát adják meg, és nem az élességállítási távolságét (változatos, sokszor hibás elnevezésekkel illetve azt).
Belépőpupilla, fényerő
A belépőpupillán keresztül jut be a fény az objektívbe. Egyetlen lencse esetén a belépőpupilla helye és a lencse fősíkja gyakorlatilag egybeesik, a belépőpupilla átmérője pedig a lencse hasznos átmérője. Összetett objektívek esetén a helyzet sokkal bonyolultabb, ilyenkor a belépőpupilla csak virtuális, általában a fényrekeszről (lásd lejjebb) alkotott virtuális kép. A belépőpupilla mérete kihat mind a lencse fénygyűjtő képességére, mind a fénykép élességi viszonyaira.
Képzeljünk el két tárgypontot, amelyek ugyan önálló fényforrásként foghatók fel, de olyan közel vannak egymáshoz, hogy a fényképen nem tudjuk őket megkülönböztetni (digitális fényképezőgépnél ezt nyugodtan mondhatjuk úgy, hogy egy pixelre esnek). A fényérzékeny felület megvilágítása az egységnyi felületre jutó fényáramtól függ. Az előző anyagokból tudjuk, hogy az oldalnagyítás határozza meg, mekkora felületen terülnek szét ebből a két tárgypontból származó fénysugarak, amely így kihat az objektív által vetített kép világosságára (egy adott megvilágítási időt feltételezve pedig magára az expozícióra). Tanulmányozzuk most egy kicsit jobban az oldalnagyítás függését a tárgytávolságtól és a gyújtótávolságtól:
|
1 / f = 1 / k + 1 / t |
a leképzési törvény a kiindulópont |
|
k = 1 / ( 1 / f – 1 / t ) |
a képtávolságot kifejezve |
|
N = K / T = k / t |
az oldalnagyítás kiszámításának képlete |
|
|
|
|
1 |
|
|
N = ────────── |
helyettesítsük be k helyére az előbb kifejtett képtávolságot |
|
( 1 / f – 1 / t ) * t |
|
|
|
|
|
1 |
|
|
N = ───── |
a nevezőben a t -vel való szorzást elvégezve |
|
t / f – 1 |
Ellenőrizzük a képletet egy ismert esettel, amikor az oldalnagyítás 1-szeres. Ilyenkor tudjuk hogy a tárgytávolság a gyújtótávolság kétszerese.
|
1 |
|
|
N = ───── |
t helyére behelyettesítve 2f -t |
|
2f / f – 1 |
|
|
N = 1 |
a képlet igazolta az egyszeres oldalnagyítás felételét |
Mit is jelent ez? Ha a tárgytávolság sokszorosa a gyújtótávolságnak (t >> f) akkor a t / f hányados nagy értékű lesz, ez fogja meghatározni a nevező értékét, a -1 jelentéktelenné válik. Ha a tárgytávolságot rögzítjük ezen a magas értéken, a gyújtótávolsággal közel egyenesen arányos lesz az oldalnagyítás. Nézzünk erre egy példát:
ha f1 = t / 100 (ez életszerű, pl. 5m a tárgytávolság és 50mm a gyújtótávolság) akkor N1 = 1 / ( 100 – 1 ) = 1 / 99 = 0,0101
ha f2 = t / 50 (kétszeresére nőtt a gyújtótávolság, az előbbi példa alapján 100mm-re) akkor N2 = 1 / ( 50 – 1 ) = 1 / 49 = 0,0204
f2 / f1 = ( t / 50 ) / ( t / 100 ) = 2 N2 / N1 = 0,0204 / 0,0101 = 2,02 2 ≈ 2,02
Láthatjuk, hogy változatlan tárgytávolság esetén kétszeres gyújtótávolság hatására közel kétszerese lett az oldalnagyítás, ami egyenes arányosságnak tekinthető. Az oldalnagyítás kétszerezésével, ugyanazoknak a fénysugaraknak kétszer olyan hosszan kell elterülniük. Mivel a kép kétdimenziós, mindkét dimenzió mentén kétszeres növekedés négyszer akkora felületet jelent. Tehát ha megduplázzuk a gyújtótávolságot, a lencse pedig ugyanannyi fényt képes begyűjteni, akkor a kétszeres oldalnagyítás miatt négyszer nagyobb felületen oszlik el a fény, így a kép sötétebb lesz (a példaként felhozott két tárgyponthoz tartozó képpont esetében ez azt is jelenheti, hogy nem egy pixelre esnek, így talán könnyebb elképzelni, miért lesz sötétebb a vetített kép). Amennyiszer nagyobb felületre terül a kép, annyiszor több fényt kell beengedni, hogy ne legyen sötétebb a kép. Egy dimenzió mentén gondolkodva: annyiszor nagyobb átmérőjű belépőpupillára van szükség, amennyiszer nagyobb az oldalnagyítás.
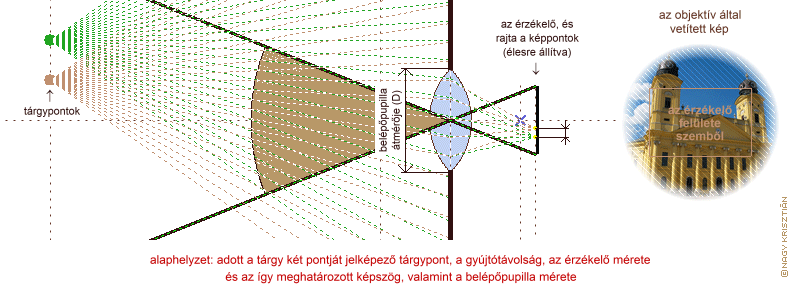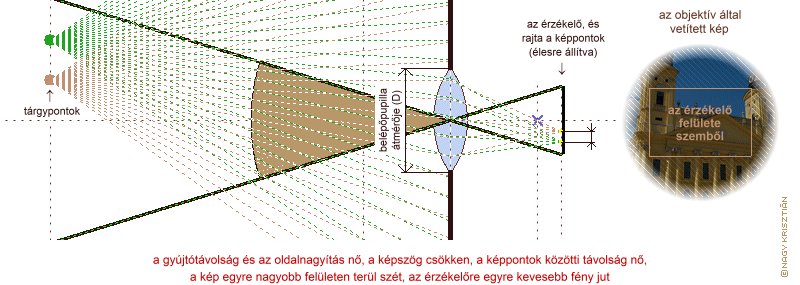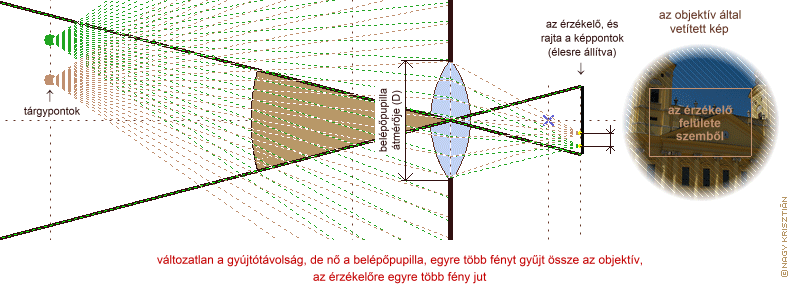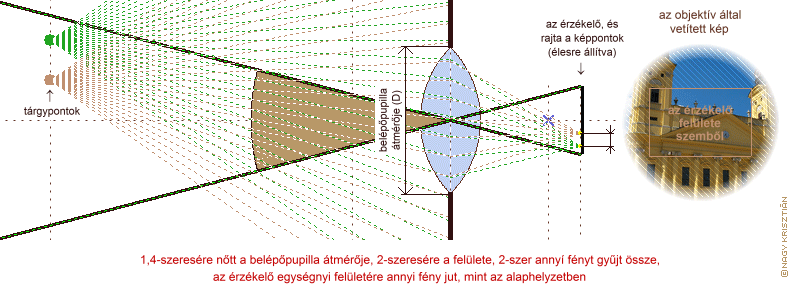
a belépőpupilla és a gyújtótávolság egymáshoz való viszonyának következménye
Úgy is fogalmazhatunk, hogy ha ugyanazokat a tárgyakat ugyanolyan világosan szeretnénk a fényérzékeny felületen látni, akkor a gyújtótávolság és a belépőpupilla méretének arányát állandó értéken kell tartani. Ezt az összefüggést fejezi ki a nyílásviszony, a belépőpupilla átmérőjének és a gyújtótávolságának aránya, amelyet az objektív fényerejének jellemzésére használnak.
|
D |
belépőpupilla átmérőjének jele |
|
D : f |
a nyílásviszony |
|
1 : f/D |
ez a forma gyakoribb, tehát az arányosság osztva D-vel |
Példa: ha egy 100mm gyújtótávolságú objektív belépőpupillájának átmérője 25mm, akkor nyílásviszonya 1 : 100mm / 25mm vagyis 1 : 4
Ebből következik, hogy egy lencsénél a kívánt nyílásviszony és gyújtótávolság meghatározza a lencse átmérőjét. Összetett lencserendszerek, objektívek esetén ez általában nem igaz, mert a belépőpupilla nem testesül meg fizikailag, nem azonos egyetlen lencse átmérőjével sem, de vannak olyan esetek, amikor jól tetten érhető az összefüggés. Ilyenek például a nem változtatható (fix/prime), nagy gyújtótávolságú teleobjektívek, és az egyszerű felépítésű, kis és közepes fényerejű fix objektívek első lencséi. A valóságos gyújtótávolság és fényerő gyakran kis mértékben eltérnek a feltüntetettektől, ezért nem igazolja pontosan számításunkat a lencse átmérője.
Változtatható gyújtótávolságú (zoom) objektíveknél gyakran előfordul, hogy a fényerő változik a gyújtótávolság függvényében, ezért ilyenkor a két szélsőértéket adják meg. Pl. a 70-300 mm 1:4-5.6 jelölés azt jelenti, hogy 70 mm-es állásban 1:4, míg 300 mm-es állásban 1:5,6 a fényerő.
A fényerő meghatározása az expozíció helyessége szempontjából döntő jelentősséggel bír. A különböző konstrukciójú és különböző képszögre tervezett objektívek azonos számított fényerő mellett más és más expozíciót eredményeznének. Ezért a korszerű objektíveknél, a fényerő megadásánál az értéket korrigálják a veszteségekkel, illetve eleve úgy tervezik az objektívet, hogy az elérni kívánt fényerő már a korrigált legyen.
Fényrekesz, rekeszszám
A fényrekesz (angolul: diaphragm, aperture-stop – németül: lichtblende, blende) egy olyan nem átlátszó anyagból készült szerkezet, amely akadályt jelent a tárgyakról kiinduló fénysugarak számára. Használatával egy optikai tengellyel koncentrikus lyuk jön létre, amelynek átmérője állítható, és így a fénynek csak egy része juthat be az objektívbe. Hatása és feladata alapvetően megegyezik a szemünkben lévő szivárványhártyáéval.

a fényrekesz megváltozásának hatása
A fényrekesz átmérője meghatározza a belépőpupilla átmérőjét. Egyetlen lencséből álló objektív esetén a fényrekesz közvetlenül a lencse előtt helyezkedik el, és ilyenkor a fényrekesz maga a belépőpupilla. Összetett objektívek esetén, a fényrekesz az objektív belsejében van, és így a belépőpupilla a fényrekeszről alkotott virtuális kép. A rekeszszám (f-number) vagy rekeszérték, és az objektív fényereje rokon fogalmak. Míg a fényerő az objektív konstrukciós adata, és a legnagyobb belépőpupillához tartozó nyílásviszonnyal jellemezhető, addig a rekeszszám az aktuális belépőpupilla átmérőből számított nyílásviszonyból ered. Számításának módja: f / D (vegyük észre, hogy ez ugyanaz, mint a D-vel osztott nyílásviszony jobb oldala). Jele a nemzetközi szakirodalomban: f/#, írásmódjában általában az f/… jelölést alkalmazzák, pl.: f/8. A fényerő egyben meghatározza a legnagyobbra nyitott rekeszhez tartozó rekeszszámot. A gyártók gyakran a legnagyobb átmérőjű fényrekeszt jelölik meg a nyílásviszony helyett az objektíven, de egyéb jelölések is elterjedtek. Ennek csak formai jelentősége van, számszerűleg az értékek ugyanazok.
Példa: 1:4 fényerejű objektív legnagyobb átmérőjű rekeszének jelölése: f/4
a fényerőt így jelölhetik az objektíveken: 1:4, f/4, f4, /4, 4
A rekeszszámot általában diszkrét lépésekben lehet változtatni. Bármekkora is a lépésköz, a rekeszszámok egy mértani sorozat elemeit képezik. Az un. teljes lépésközű sorozat szomszédos értékei kétszeres keresztmetszetet jelentenek, amely egyenes arányosságban áll az áteresztett fénnyel. Mivel az átmérő és a felület között négyzetes az összefüggés, ebből következik, hogy a rekeszszámok sorozatának hányadosa kettő négyzetgyöke, vagyis kb. 1,41. Az objektíveken illetve a fényképezőgépeken általában köztes értékek is beállíthatóak. Ha 1/2 a lépésköz, akkor a sorozat hányadosa 21/4, 1/3 lépésköz esetén pedig 21/6. A fényrekesz idegen nyelvű elnevezései miatt gyakran a „stop” vagy a „blende” kifejezést használják a rekesz változásának jellemzésére. Pl. a „2 stop” vagy „2 blende” négyszer annyi vagy negyed annyi fényt jelent attól függően, hogy növeltük vagy csökkentettük a fényrekesz átmérőjét. Egyes esetekben a külső fényviszonyok változását is úgy fejezik ki, hogy azt mekkora fényrekesz-változással lehetett volna elérni. A korszerű, elektronikus vezérlésű objektívek rekeszbeállító mechanikája egészen finom lépésekre is képes.
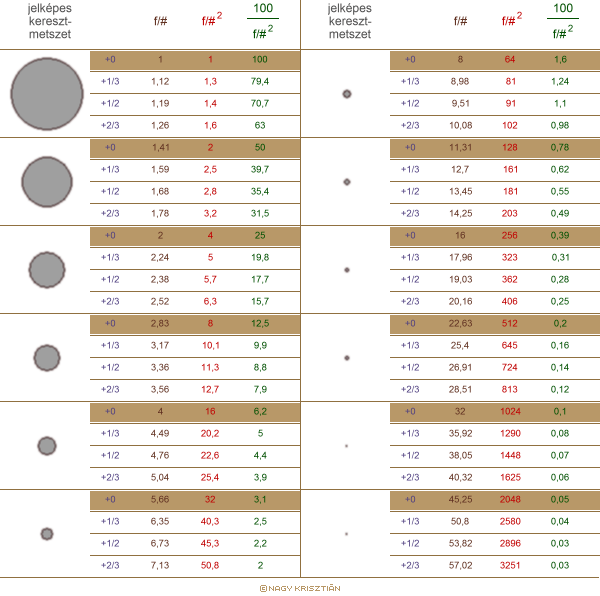
számított rekeszszám sorozat 1/2 és 1/3 lépésközzel
A teljes lépéseket tartalmazó sorozathoz csak a „+0” sorokat kell a fenti táblázatból összeolvasni, pl.: 1,41 ; 2 ; 2,83 ; 4 … A fél lépésközt alkalmazó sorozatnál be kell szúrni az egészek közé a „+1/2” sorokat, pl.: 4 ; 4,76 ; 5,66 ; 6,73 ; 8 ; … A harmad lépésközű sorozathoz a „+0” értékek közé a „+1/3” és a „+2/3” sorokat kell beszúrni, pl.: 2,83 ; 3,17 ; 3,56 ; 4 ; 4,49 ; … A táblázatban a pontos, számított rekeszszámok kerültek feltüntetésre, azonban ezek jelölésére a kerekített (vagy inkább a csonkított) értékeket használják: 1 ; 1,4 ; 2 ; 2,8 ; 4 ; 5,6 ; 8 ; 11 ; 16 ; 22 ; 32 ; 45. A fényképezőgépekben lévő automatika azonban a pontos értékekkel számol és az objektívnek is pontos értéket ad át, csak a kijelzőn jelenik meg a kerekített adat! A rekeszszám négyzete felhasználható annak kiszámítására, hogy hányszorosára kell növelni a megvilágítás hosszát (záridő) az azonos expozíció érdekében.
Példa: Hányszorosára kell növelni az 1/800 másodperc megvilágítási időt, ha a rekeszérték F4-ről F7,1-re változik?
f/4 rekeszre: 42 = 16 f/7,1 rekeszre: 7,132 = 50,8 50,8 / 16 = 3,175
Tehát 3,175-szörösére kell növelni a megvilágítás idejét, így 1/800 másodpercről 1/250 másodpercre kell változtatni.
Az utolsó oszlopban lévő érték f/1 fényrekeszhez viszonyítva mutatja a keresztmetszetet (és így a beeresztett fényt is) %-ban. A névleges, pl. egy objektív adatai között feltüntetett fényerő, és a rekeszszámok is végtelen távolságra lévő tárgyakra vonatkoznak, kiszámításukhoz csak a gyújtótávolságot és a belépőpupilla méretét használjuk fel. A fényerőnél tárgyaltakból azonban kitűnik, hogy az oldalnagyítás, amely döntő hatással van az érzékelőre vetített kép világosságára, csak akkor áll megközelítően egyenes arányosságban a gyújtótávolsággal, ha a tárgytávolság a gyújtótávolság sokszorosa. Közeli tárgy (pl. makrofényképezés) esetén az oldalnagyítás jelentősen megnő, ezért az érzékelő egységnyi felületére kevesebb fény jut. A pontos expozícióhoz nem a névleges, hanem az adott helyzetben aktuális fénygyűjtő képességre utaló értéket kell használni, az un. effektív rekeszszámot (working f-number). Kiszámításának módja: f/#eff. = f/# * ( 1 + N ) ahol N az oldalnagyítás. Általános esetben a tárgytávolság jóval nagyobb, mint a gyújtótávolság, N < 0,1 így f/#eff. ≈ f/#, tehát nincs lényeges különbség a névleges és az effektív érték között. Egyes fényképezőgép-objektív kombinációk esetében a névleges, míg másoknál az effektív rekeszszámot jelenítik meg (pl. a státusz kijelzőn). Minden tükörreflexes vagy kompakt digitális fényképezőgép objektíven keresztül mér fényt (TTL) ezért nem okoz expozíciós hibát az effektív és a végtelenre számított rekeszszám eltérése.
Példa: Egy 1:2,8 fényerejű objektívet makrofényképezésre használunk. Az élesre állított tárgysíkon elhelyezkedő tárgyat 1:1 nagyítással szeretnénk lefényképezni. Ha teljesen kinyitott fényrekesszel fényképezünk, mekkora lesz az effektív rekeszszám?
1:2,8 fényerőhöz tartozó teljesen kinyitott fényrekesz: f/2,8
Ha N = 1 akkor 2,8 * ( N + 1 ) = 2,8 * ( 1 + 1 ) = 5,6
Tehát 5,6 az effektív rekeszszám, negyed annyi fényt gyűjt az objektív, mint végtelenre állított esetben. Ez a táblázatból is kiolvasható, ha a beeresztett fényt összehasonlítjuk f/2,8 és f/5,6 esetében.
megjegyzés: Az Optika I. anyagban rögzítettük, hogy az egyszerűbb megértés kedvéért a távolság és méretadatokat előjel nélkül tárgyaljuk. Amennyiben a lencse viselkedését egy koordinátarendszerben vizsgáljuk, az előjeleknek fontos szerepük lesz, pl. a tárgymagasság és a képmagasság ellenkező előjelű, hiszen a tárgypontot az optikai tengely túloldalára vetíti a lencse. A nagyítás így negatív lesz, és ezért találkozhatunk a szakirodalomban az effektív rekeszszám képletével f/# * ( 1 – N ) formában.
Gyakorlati kivitele szempontjából a fényrekesz lehet toló, revolver és írisz. Kisformátumú digitális fényképezésben szinte kizárólag az írisz fényrekeszt használják, amely két oldalon csapágyazott köríves lamellákból áll. Szabályos körív esetén a nyitott fényrekesz megközelítően tökéletesen kör alakú, de szűkítésével egyre inkább sokszögformát ölt. A jelenség akkor igazán feltűnő, ha csak 5-6 db lamellát használnak. Bár a lamellák speciális formai kialakításával lehet ezen segíteni, a kis számú lamellából álló íriszek nyoma mindig felfedezhető a képen azoknál a tárgyaknál, amely nem voltak élesre állítva. Ilyenkor a kisebb fénypontok, pl. levelek között átszűrődő fény vagy távoli lámpák fénye nem kör, hanem sokszög alakú foltot hagynak a képen. A régebbi, manuális működtetésű objektíveknél előfordult, hogy 20 feletti volt a lamellák száma.
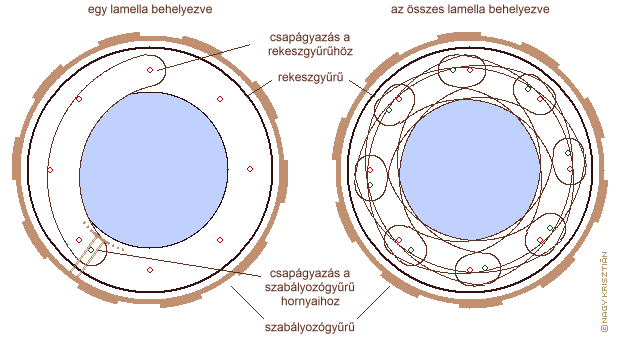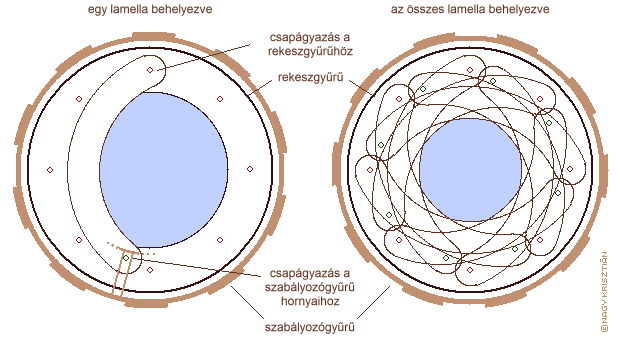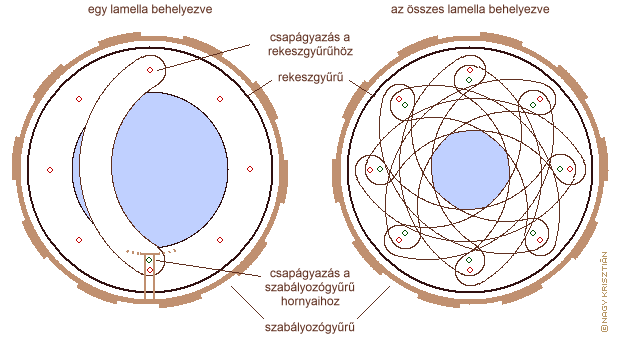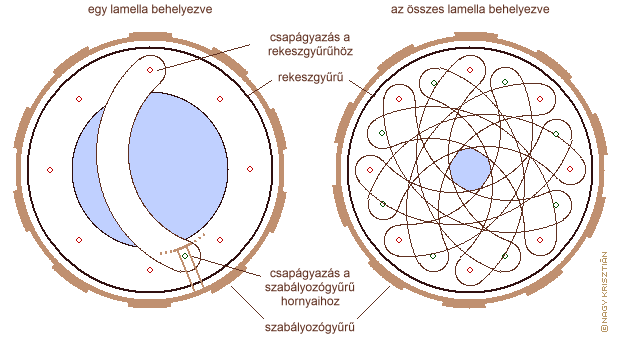
az írisz fényrekesz felépítése és működése (8 lamellás)
Az írisz fényrekesz továbbfejlesztése nagymértékben hozzájárult a fényképezőgépek automatizálásához. A beugró-fényrekesz alapállapotban teljesen nyitott, csak az expozíció időtartama alatt húzódik össze annyira, amennyire azt a beállított rekeszszám megkívánja. Ennek több előnye is van: az élességállítás és komponálás alatt a lehető legtöbb fény jut be a fényképezőgépbe, ezért mind az automata mind a manuális élességállítás könnyebb, illetve világosabb a kép a keresőben. A beugró-fényrekesz alkalmazását a gyártók régebben „AUTO” vagy egyéb felirattal jelölték az objektíveken, de ma már olyan alapvető tulajdonság, hogy nem tüntetik fel külön. Fontos, hogy a lamellák a lehető legjobban elnyeljék a fényt, ellenkező esetben hozzájárulnak az objektíven belüli tükröződéshez, amely káros hatással van a kép minőségére
A fényrekeszekhez is kapcsolódik egy tévhit, nevezetesen az, hogy a beállított rekeszszámtól függhet az automata élességállítás pontossága. A beugró-fényrekesz működésének ismeretével kijelenthető, hogy ez hamis állítás, hiszen az élességállítás teljes ideje alatt a fényrekesz maximálisan nyitott állásban van. Ha az élességi viszonyok mégis megváltoznak, annak két oka lehet:
- egy objektív képalkotási hiba (szférikus aberráció) következtében létrejövő fókusz eltolódás
- a kisebb átmérőjű fényrekeszhez tartozó nagyobb mélységélesség elfedi a hibás élességállítást (lásd következő anyag)
A fényrekesz pillanatnyi állapotát gyakran jellemzik a „szélesre nyitott, teljesen kinyitott” (wide-open) vagy a „lerekeszelt” (stopped-down) kifejezésekkel.