A digitális képérzékelésre ugyanúgy vonatkoznak a mintavételezés törvényei, mint más mintavételezéssel működő eljárásokra. Célunk az eredeti kép reprodukálása, azonban ez feltételekhez kötött. Végtelen mennyiségű képi információt nem lehetséges véges mennyiségű érzékelési pont (pixel) segítségével rögzíteni, tárolni. Amennyiben a mintázat sűrűsége átlép egy határt, úgy a mintavételezés – azaz a pixelekre bontás – információveszteséggel jár, sőt gyakran jól látható, hamis mintázat keletkezik. Az angol nyelvben e képi jelenségre használt „pattern” (minta) és a mintavétellel kapcsolatos „sample” (minta) szavak jól elkülönülnek. Annak érdekében, hogy e magyar nyelvű szövegben is így történjen, előbbire következetesen a „mintázat” szót fogjuk használni.
Az alábbi tesztképen az egyes oszlopokban különböző térfrekvenciájú mintázat van, amelyet egy szimulált képérzékelésnek vetünk alá. A térfrekvencia nem más, mint a világos és sötét sávok hosszegységre eső száma, amelynek mértékegysége: ciklus/mm vagy vonalpár/mm.

az eredeti tesztkép

a pixelek így fedik le a képet (a vékony vonalak a pixelek határait mutatják) példánkban a tesztkép 140×35 pixel felületre vetül az érzékelőn
A 7. oszlop nevezetes, az ebben lévő mintázat térfrekvenciája megegyezik az un. Nyquist-frekvenciával (FNyquist), amely nem más, mint a mintavételi frekvenciának (pixel/mm) a fele. A mintavételi törvények ehhez a határhoz kötik az információ reprodukálhatóságát. A zárójelben lévő számok azt mutatják, hogy a Nyquist-frekvenciának hányszorosa a tesztképen függőlegesen mérhető térfrekvencia. Ezek a tesztábrán egy mértani sorozatot alkotnak, ahol a hányados 21/3, így FNyquist negyedénél, felénél és kétszeresénél illetve köztes értékeken is megfigyelhető a mintavétel eredménye.

a mintavételezett kép, ahol a pixelen belüli részletek átlagolódtak – 140×35 pixel
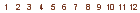

a mintavételezett kép nagyítás nélkül – 140×35 pixel
Az szimuláción jól látható, főleg a 8, 9. és 11. oszlopban (tehát mindhárom esetben a 7. oszloptól jobbra, FNyquist-tól nagyobb értéken), hogy olyan mintázat keletkezett, ami az eredeti képben nem volt benne. Ennek oka az átlapolás, angolul: alias, magát a hamis mintázatot, pedig moire-nek nevezik. (meg kell jegyezni, hogy a moire egy jóval szélesebb körben használt fogalom, különböző képi interferenciajelenségekre használják, de a mintavételezési hibák eredményét is így hívják). A túl nagy frekvenciájú jel számára FNyquist egyfajta tükör. Amennyivel nagyobb nála a mintavétel előtt, annyival lesz kisebb utána (FNyquist kétszereséig, majd újra fordul az irány). Ez a jelenség megfigyelhető a 3. és a 9. oszlopban, mivel ezek kb. 0,6*FNyquist-val térnek el a Nyquist-frekvenciától, csak ellentétes irányban. Ezért beszélünk információvesztésről átlapolásnál, hiszen mi most csak azért tudjuk, hogy ott eredetileg milyen térfrekvenciájú jel volt, mert mi hoztuk létre az ábrát. A valóságban azonban az a helyzet, hogy a mintavétel után rendelkezésre álló információból nem lehet eldönteni, hogy az eredeti jel vagy átlapolás következménye.

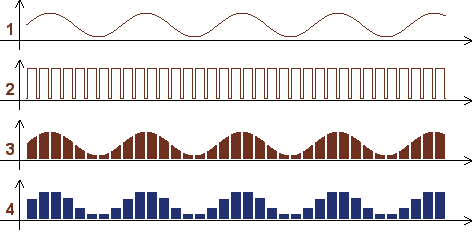

a mintavételezés folyamata abban az esetben, ha a mintavételi frekvencia megválasztása helyes (az 1. és 4. görbe egyformán periódikus, nincs átlapolás)
A jelfeldolgozásban a mintavétel után létrejött jelet egy forrás jel (1) és egy mintavételi függvény (2) szorzataként (3) írják le. Például digitális hangrögzítés esetén a mintavételi függvény nagyon keskeny impulzusok sorozata, tehát az időben változó jelből úgy vesznek mintákat, hogy a mérés ideje rövid legyen. A képérzékelőknél az előbbi impulzusok (természetesen itt nem időben, hanem térben változó a jel) gyakorlatilag összeérnek (2). Ennek oka, hogy az érzékelő felületén a pixelek, pontosabban a felettük lévő mikrolencsék a lehető legnagyobb felülettel rendelkeznek, hiszen így lehet a legtöbb fotont befogni, a legjobb jel/zaj viszonyt elérni. Ennek következménye, hogy a pixelre vetülő információ átlagolódik (4), és így az átlapolás miatt keletkező moire amplitúdója a frekvencia emelkedésével periódikusan csökkenő jellegű. (pontosabban a sin(ω)/ω függvény írja le). Ez az oka annak, hogy a tesztábrán még FNyquist többszörösénél nagyobb térfrekvencián is keletkezik átlapolás, de kisebb mértékű, mint alacsonyabb térfrekvencián. (11. és 12. oszlop) Természetesen, ha átlós irányban vizsgáljuk a helyzetet, négyzetes pixelek esetén a Nyquist-frekvencia csak a 0,7-szerese a vízszintes vagy függőleges értéknek.

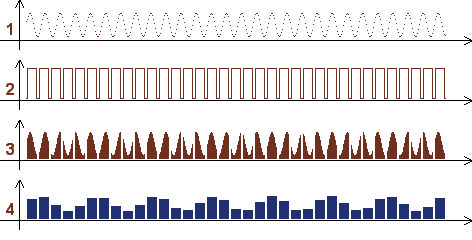

a mintavételezés folyamata abban az esetben, ha a mintavételi frekvencia megválasztása helytelen
(a 4. görbe itt is periódikus, de látszólag jóval kisebb a térfrekvencia, mint az 1. görbén, mert átlapolás keletkezett)
Az átlapolás elkerülése érdekében korlátozni kell a mintázat térfrekvenciáját. A valóságban ez egy un. antialias (AA) filter, vagyis átlapolásmentesítő szűrő segítségével történik, amelyet az érzékelő előtt helyeznek el. Az AA filter gyakorlatilag egy nagyon precíz homályosítást (blur) végez. Egy szimulált AA szűrővel az átlapolás csökkenése és így a moire változása is jól láthatóvá válik. Az alábbi két szűrt kép a GIMP program Gaussian Blur szűrőjével készült, eltérő rádiusszal.
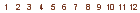  AA nélkül |
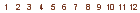  enyhe AA |
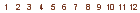  erős AA |
A szűrésnek alávetett képeken jól látszik, hogy a moire csökkent vagy megszűnt. Érdemes megfigyelni, hogy miközben a nagyon sűrű mintázat szinte homogén felületté vált, a közepesen sűrű mintázat jobban hasonlít az eredeti képhez.
Ezen a ponton érdemes szétválasztani a moire és az AA vizuális hatását a matematikai/fizikai hatástól. Sokan vannak, akik az AA szűrők teljes elhagyását tekintenék hasznosnak. Ez részben indokolható azzal, hogy az AA homályosító hatása hozzáadódik az objektívek képalkotási hibáihoz. Az egyre nagyobb felbontású érzékelők, egyre kisebb pixelek, és a kisfilmes objektíveknek a kisfilmtől kisebb érzékelőn való használata eleve kiélezett feladat elé állítja az optikai rendszert. Tény, hogy az AA szűrés nélkül készült képeken a vékony vonalak élesebbnek látszanak. Továbbá azt is figyelembe kell venni, hogy a szemünk és az agyunk könnyen becsapható. A sűrű mintázatot, mint például egy ember haját, vagy egy madár tollazatát lefényképezve AA szűrő nélkül, a moire-t nem mindig érzékeljük hibának, úgy látjuk, mintha azok is valós részletek lennének.
Szubjektív véleményem, hogy az AA szűrő elhagyását részben az is erőlteti, hogy a kép minőségének ellenőrzésére olyan amatőr szempontok terjedtek el, amelyek túlzóak és nem feltétlenül a valóság visszaadását segítik a fénykép által. Gyakran hallható, hogy a képet 100%-ra nagyítva (tehát amikor egy képpont a képernyőn megfelel egy képpontnak a képfájlban) a kontúrok határozottsága alapján döntik el, mi éles és mi nem. Bár AA nélkül valóban élesebbnek látszik az így készült kép ekkora nagyításban, az egész képet felhasználva (pl. egy nagyméretű nyomtatás) a matematikailag is pontosabb kép közelebb fog állni a valósághű látványhoz. A képalkotási hibák, és egyéb tényezők miatt a megoldás valahol félúton van.
A példákban eddig csak egyszínű érzékelésről esett szó, de a helyzetet jelentősen bonyolítja, hogy alapvetően színes kép előállítása az igény. Színes kép érzékeléséhez legelterjedtebben a Bayer CFA-val ellátott érzékelőket használják.
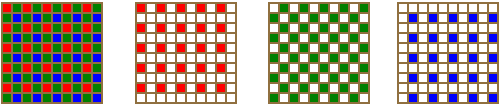
A Bayer CFA felépítését figyelve megállapítható, hogy a kék és vörös színcsatorna esetén minden irányban feleződik a mintavételi frekvencia (és így FNyquist is) a monokróm érzékelőhöz képest. A zöld színcsatornán a függőleges és vízszintes irányban szintén feleződik, átlósan viszont nem változik. Mindezek következménye, hogy a színes digitális fényképezőgépeknél már a pixelek sűrűségét megközelítő mintázatnál megjelenik a moire, gyakran hamis színekkel kísérve (szivárványos részletek a képen). A helyzetet azért enyhíti, hogy a színcsatornák nem függetlenek egymástól, így a kép világosságáról több információ áll rendelkezésre.

a Bayer CFA-val ellátott érzékelő ennyit rögzít a tesztképből
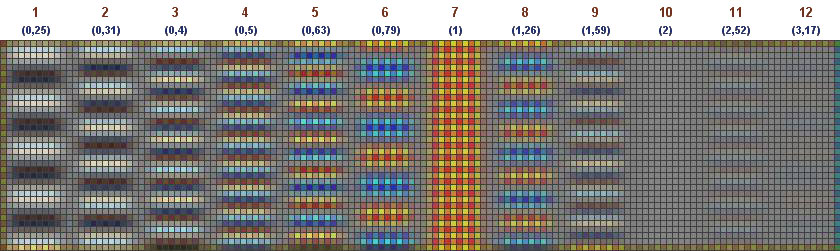
bilinear demosaic eljárással visszaállított kép
(ennél az eljárásnál a színcsatornák függetlenül vannak kezelve)
  AA nélkül |
  enyhe AA |
  erős AA |
Az 5-8. oszlopok között színes moire vehető észre. Ennek legfőbb oka az, hogy a létrejövő moire itt eltoltan jelentkezik az egyes színcsatornákon, amelyek nincsenek egymással fedésben, hiszen a vörös, zöld és kék pixelek egymás közé ékelődve helyezkednek el. Ezért az eredetileg szürke árnyalatból színes pixelek keletkeznek. A hamis színek is jelentősen csökkennek az AA szűrő alkalmazásával.
A moire jelenléte egy fontos dologra enged következtetni: az optikai rendszer felbontása elég nagy ahhoz, hogy az érzékelő felbontásánál nagyobb felbontású kép előállítására is alkalmas legyen. Ha az objektív életlen képet vetít az érzékelőre, nem keletkezhet moire. Tehát ha hamis mintázatot és színes pixeleket tapasztalunk a kép finom részleteinél, azt jelenti, hogy az objektívünkben még vannak tartalékok.
Mi a tökéletes megoldás az átlapolás problémájára, amely a lehető legtöbb információt őriz meg a képből? A válasz egyszerű: a lehető legnagyobb mintavételi frekvencia, azaz a lehető legnagyobb képfelbontás. Ha a pixelek teljes és hasznos felületének arányát (pixel fill factor) sikerül változatlanul magas értéken tartani a pixelek méretének csökkenése esetén is, akkor azonos képfelbontásra méretezve a képeket a jel/zaj viszony nem változik, így az egyre nagyobb felbontás nincs kedvezőtlen hatással a képminőségre. Előnyökkel azonban járhat:
- következmények nélkül elhagyható az optikai AA szűrő
- a részletek valósághű visszaadását valóban csak az objektív képességei korlátozhatják
- digitális úton olyan tökéletes AA szűrés végezhető a kép átméretezése előtt, amelyre optikai úton nincs esély.
A felbontás növelését az is indokolja, hogy a Nyquist frekvencia egy idealizált határ. A példában nem vettük figyelembe, hogy az információ mindig torzul, pl. zaj adódik hozzá. Nem tudható, hogy a képérzékelő-technológia merre fejlődik tovább. Mivel a Bayer CFA a fényenergia jelentős részét elpazarolja, elképzelhető, hogy néhány év múlva a mai Foveon-technológiához hasonló többrétegű érzékelők terjednek majd el, amelyekkel minden színcsatornán azonos a mintavételi frekvencia. Ilyen kutatások jelenleg is folynak, szerves alapú érzékelőkkel.
Felmerülhet a kérdés, hogy a tesztábrákon a periódikusan ismétlődő mintázat miért nem egyszerűen fekete és fehér vonalakból áll, miért szinusz alakú a világossággörbe. Ez azért van, mert a váltakozó vonalaknak megfelelő négyszögjel matematikailag egy végtelen számú komponensből (harmonikus rezgésből) álló függvény, ezért bonyolultabb lett volna a Nyquist-frekvenciával összevetni. A négyszögjel függvénye a következőképpen írható le:
f(t) = C + A*(sin(ωt) + sin(3ωt)/3 + sin(5ωt)/5 + sin(7ωt)/7 + sin(9ωt)/9 + sin(11ωt)/11 + sin(13ωt)/13 ……. )
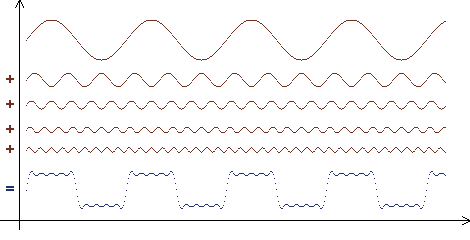
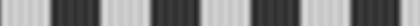
az alapharmonikus és az első négy felharmonikus összegéből már jól felismerhető a négyszögjel (és a szinuszos tesztábrához képest határozottabb, élesebb kontúrok, váltakozó világos és sötét vonalak)
Tehát a négyszögjel az alapharmonikus páratlan egész számú többszöröseit is tartalmazza, egyre csökkenő amplitúdóval. Ugyanilyen okból az objektívek felbontóképességének jellemzésére használt modulációs transzferfüggvény (MTF) kiszámításának képleteiben korrekciós tényezők is vannak, amennyiben azt nem szinuszos tesztábrán mérik.










