Szóródási kör és mélységélesség
Az élességállításnál tárgyaltakból kitűnik, hogy egy beállított kihuzathoz egyszerre mindig csak egy olyan tárgytávolság tartozik, amely esetén a fényérzékeny felületen pontként jelennek meg a tárgypontok. Ilyenkor tökéletesen éles a kép, és az élesen leképzett pontok egy nevezetes tárgysíkot, az élesség síkját határozzák meg. Azok a tárgypontok, amelyek ennél közelebb vagy távolabb helyezkednek el, a lencse (pontosabban a pupilla) keresztmetszetének megfelelő foltként jelennek meg a fényképen. Ezt a foltot szóródási körnek nevezzük. Angolul: CoC = Circle of Confusion. Az így létrejövő szelektív élesség egy rendkívül fontos tényezője a fénykép készítésének. Lehet nagyon fontos kompozíciós eszköz a téma háttérből való kiemeléséhez (éles téma – homályos háttér), de lehet nem kívánatos következmény is, amikor nem tudjuk a fényképezőgéptől különböző távolságra lévő tárgyakat egyszerre élesnek mutatni.
Belátható, hogy nem csak azt a tárgypontot fogjuk élesnek látni, amely abszolút pontszerűen képződik le (szóródási kör átmérője nulla). Sem a szemünk, sem a kép rögzítésére szolgáló eszköz nem alkalmas arra, hogy végtelen pontossággal meghatározza a szóródási kör átmérőjét. Meg kell jelölnünk egy határt, amelytől nem nagyobb szóródási kört még élesnek tekintünk.
A magyar nyelvű szakirodalom nem egységes a mélységélességhez kapcsolódó fogalmak jelölésében. Az angol szakkifejezések és rövidítések jobban elterjedtek, ezért ezeket fogjuk használni. A CoC rövidítést (sajnos nem igazán következetesen) egyaránt használják a szóródási kör pillanatnyi átmérőjének és az élességet meghatározó, elfogadott legnagyobb átmérőjének jelölésére. Azért, hogy a kettő között különbséget tegyünk, ez utóbbinak CoClim (azaz limit) lesz a jele.
Ha élesre állítjuk az objektívet egy adott tárgyra, akkor (ehhez a tárgyhoz viszonyítva) minél közelebb helyezkednek el a képen szereplő többi tárgy pontjai, annál nagyobb a hozzájuk tartozó CoC átmérője. Például ha egy arcról, szemből szeretnénk közeli felvételt készíteni egy nagy fényerejű objektívvel, és úgy állítjuk be a tárgytávolságot, hogy a szempillák tökéletesen élesek legyenek, az ajkak már kissé életlenek lesznek, az orr csúcsa pedig még jobban elhomályosodik. Ugyanez igaz, ha egyre jobban eltávolodunk az élesség síkjától. Az előző példával magyarázva: a halánték kevésbé, a fül már jobban elmosódik. A mélységélesség (DOF = Depth Of Field) annak a tartománynak a kiterjedése, amelyen belül a szóródási kör átmérője nem nagyobb, mint az általunk elfogadott határérték, ezáltal a kép részleteit élesnek tekintjük. Algebrai alakban: CoC ≤ CoClim. Kialakulását könnyen megérthetjük, ha egy pontszerű fényforrást mozgatva, egyre jobban eltávolítva az érzékelőtől megfigyeljük a rajta keletkező szóródási kör átmérőjét.
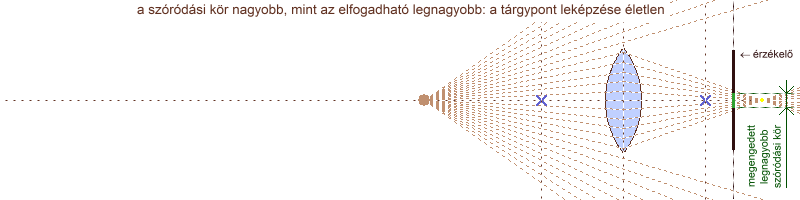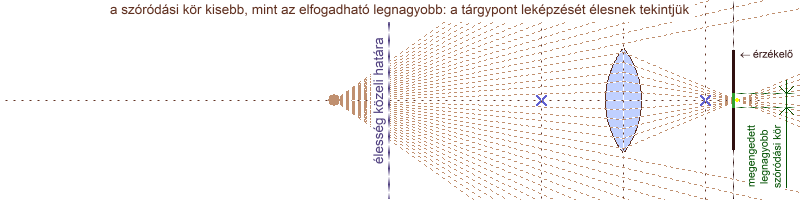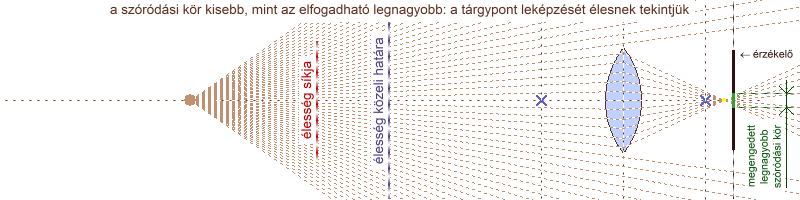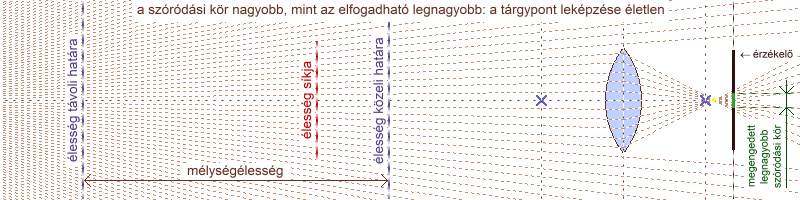
a mélységélesség kialakulása: túl közeli tárgypont esetében a lencse az érzékelő mögé, túl távoli esetében az érzékelő elé fókuszál, ezért egy folt keletkezik
A CoClim meghatározására nincs egységes módszer. A leggyakrabban alkalmazott formulák azt feltételezik, hogy bármekkorára is nagyítjuk később a fényképet, annak széleit nagyjából mindig azonos szög alatt látjuk. Egyszerűbben kifejezve: a kisebb képeket közelről, a nagyobb képeket távolról nézzük, így a kép mindig hasonlóan tölti ki a látómezőnket. Ez a feltétel és az emberi szem feloldóképessége meghatároz egy szóródási kör határértéket. A Zeiss formula szerint CoClim-t kizárólag a felvételi média (film vagy érzékelő) képméretéből származtatják, a következőképpen: CoClim = képátló / 1730. Több hasonló számítási módszer ismert, de a legjobban a képátló / 1500 formula terjedt el. A 35mm-es kisfilmen ez kerekítve 0,03mm-t jelent. Amennyiben az élesség feltételét a fénykép valamilyen más méretéhez kötik, akkor CoClim meghatározásába egyéb paraméterek is beleszólhatnak, pl. a fénykép nagyítása, a gyújtótávolság stb. Függetlenül a formulától, fontos megérteni, hogy a mélységélesség a fénykép készítésének helyszínére vonatkozik, egy olyan távolságadat, amely csak ott értelmezhető.
| Jellemzően használt CoClim méretek (közel az 1500-as formulához) | |||||||
|---|---|---|---|---|---|---|---|
| képméret jelölése | Digital 654 | 35mm-es | APS-H | APS-C | 4/3 | 1/1.7″ | 1/2.5″ |
| képátló (mm) | 60 | 43,27 | 33,75 | 26,7-28,4 | 21,75 | 9,5 | 7,2 |
| CoClim (mm) | 0,04 | 0,03 | 0,023 | 0,019 | 0,015 | 0,0063 | 0,0048 |
Ebben az írásban az objektívek gyártói által is használt, 1500-as formulát fogjuk használni. Ezt alkalmazzák általában az objektívek adatlapján megadott mélységélesség táblázatoknál, és akkor is, ha az objektívre felfestik a mélységélesség skálát. A CoClim ismerete után feladatunk a fenti animáción szereplő három nevezetes esethez tartozó távolságadatok meghatározása. Ehhez három külön ábrát kell készítenünk.


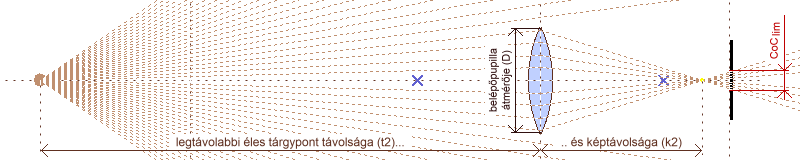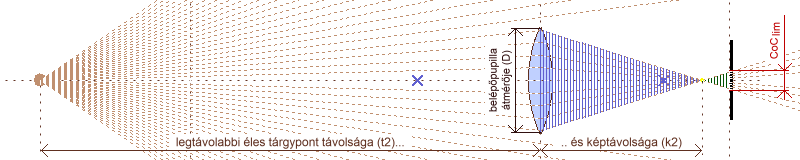
a mélységélesség számításának alapjai
|
( k1 – k0 ) / k1 = CoClim / D |
a közeli határnál a jelölt háromszögek alapján felírható aránypár |
|
( k0 – k2 ) / k2 = CoClim / D |
a távoli határnál a jelölt háromszögek alapján felírható aránypár |
|
1 / f = 1 / k + 1 / t |
újra a leképzési törvény a kiindulópont |
|
1 / k = 1 / f – 1 / t |
k -t a másik oldalra hozva (felírható k0 és t0; k1 és t1 ; k2 és t2 -re is) |
Ezekből az egyenletekből kell kiindulnunk.
|
1 – k0 / k1 = CoClim / D |
első egyenlet bal oldalán az osztást elvégezve |
|
k0 / k1 = 1 – CoClim / D |
átrendezve |
|
1 / k1 = ( 1 – CoClim / D ) / k0 |
osztva k0 -val |
|
1 / f – 1 / t1 = ( 1 – CoClim / D ) / k0 |
1 / k1 helyére 1 / f – 1 / t1 -t helyettesítve |
|
1 / f – 1 / t1 = ( 1 – CoClim / D ) ( 1 / f – 1 / t0 ) |
1 / k0 helyére 1 / f – 1 / t0 -t helyettesítve |
|
1 / f – 1 / t1 = 1 / f – 1 / t0 – CoClim / D * ( 1 / f – 1 / t0 ) |
jobb oldalon elvégezve a szorzást |
|
1 / t1 = 1 / t0 + CoClim / D * ( 1 / f – 1 / t0 ) |
1 / f -t mindkét oldalból kivonva és szorozva -1 -gyel |
|
1 / t1 = 1 / t0 + CoClim / D * ( t0 – f ) / t0f |
1 / f – 1 / t0 -t közös nevezőre hozva |
|
1 / t1 = 1 / t0 * ( 1 + CoClim / D * ( t0 – f ) / f ) |
1 / t0 -t bal oldal mindkét tagjából kiemelve |
|
t1 = t0 / ( 1 + CoClim / D * ( t0 – f ) / f ) |
mindkét oldal reciprok értéke |
|
D = f / f# |
a valóságban a rekeszszám áll rendelkezésre |
|
t1 = t0 / ( 1 + CoClim * f# ( t0 – f ) / f2 ) |
behelyettesítve megkapjuk a közeli határt |
Most a távoli határt számítsuk ki!
|
k0 / k2 – 1 = CoClim / D |
első egyenlet bal oldalán az osztást elvégezve |
|
k0 / k2 = 1 + CoClim / D |
átrendezve |
|
1 / k2 = ( 1 + CoClim / D ) / k0 |
osztva k0 -val |
|
t2 = t0 / ( 1 – CoClim * f# ( t0 – f ) / f2 ) |
t1 -gyel teljesen azonos módon végigvezetve megkapjuk t2 -t |
És végül:
|
DOF = t2 – t1 |
a mélységélesség a két határtávolság különbsége |
A közeli és a távoli határt együtt a t1;2 = t0 / (1 ± CoClim * f# ( t0 – f ) / f2) képlet adja meg, amely jellegét tekintve A / (1 ± B ) alakú. Ezt elemezve algebrai úton néhány megállapítás már most megtehető:
- a nagyobb rekeszszámok, tehát a kisebb átmérőjű fényrekesz növeli a mélységélességet

fényrekesz és mélységélesség összefüggése a gyakorlatban
Továbbá:
- az éles tartománynak az élesség síkja mögé eső része mindig nagyobb, mint ami elé esik
- minél nagyobb a ± után szereplő tag a nevezőben, annál aszimmetrikusabban oszlik el az éles tartomány az élesség síkja előtt és mögött (amit a nagy rekeszszám és a kis gyújtótávolság egyaránt elősegít)
A tárgytávolságot változó paraméterként bevezetve egy grafikonon jól nyomon követhetőek ezek a megállapítások:
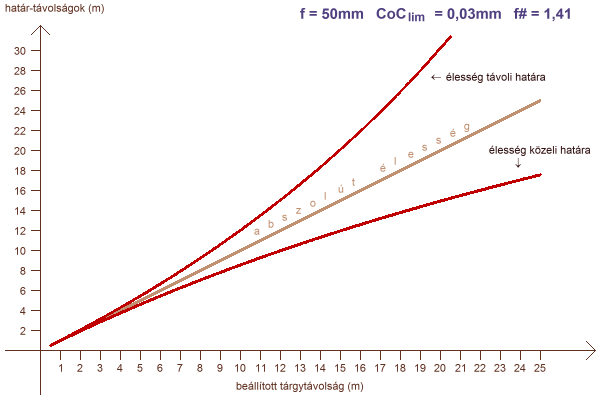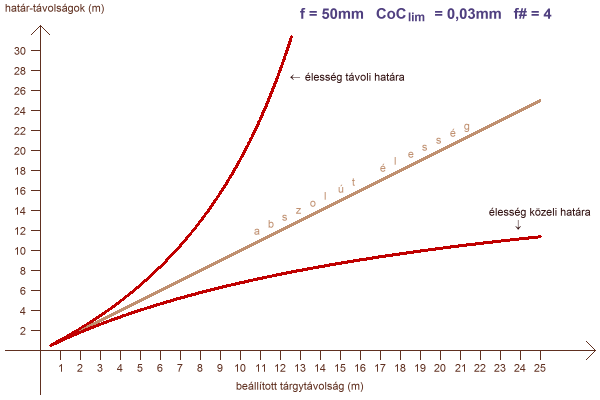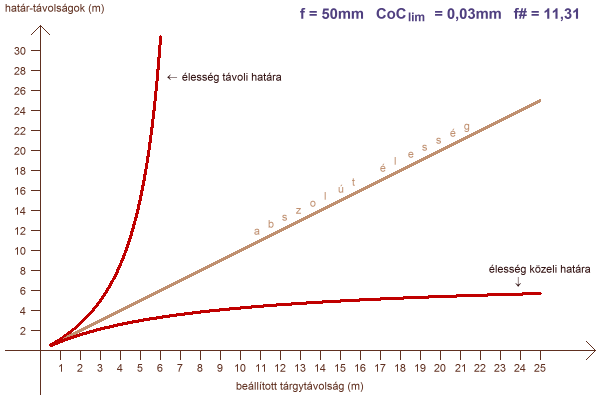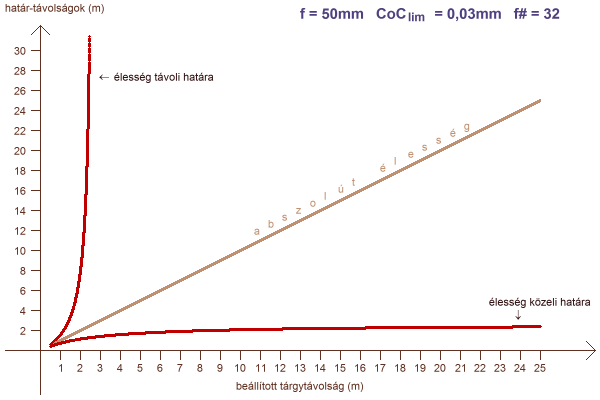
az élesség határainak alakulása a rekeszszám és a tárgytávolság függvényében
Tágra nyitott fényrekesz esetén a határvonalak nagy távolságig szinte szimmetrikusan körülölelik az élességet mutató egyenest. A fényrekesz szűkítése esetén a közeli határ lassabban, a távoli határ hirtelen elnyílik az egyenestől, így a mélységélesség hamar a végtelenbe ér.
Ehhez a fogalomkörhöz tartozik még az un. hiperfokális távolság. Ez nem más, mint az élesség közeli határa abban az esetben, ha az objektívet végtelen tárgytávolságra állítottuk be. Definíciója egyben fotográfiai jelentőségét is megmagyarázza, gondoljunk pl. egy tájkép készítésére, vagy olyan szituációkra, amikor egy mozgó témát mindenképpen az éles tartományban szeretnénk tartani, de nincs lehetőségünk gyors újrafókuszálásra. Értéke az előző egyenletekből már könnyen levezethető:
|
1 / t1 = 1 / t0 + CoClim / D * ( 1 / f – 1 / t0 ) |
a közeli határ képletének egy köztes állapotából kiindulva |
|
t0 = ∞ |
ha a beállított tárgytávolság végtelen |
|
1 / t hip = CoClim / D / f |
1 / t0 helyére 0 kerül |
|
t hip = D * f / CoClim |
mindkét oldal reciprok értéke |
|
t hip = f2 / ( f# * CoClim ) |
D helyére f / f# -t helyettesítve |
Ha a hiperfokális távolságot kiemeljük a mélységélesség képletekből, és változó paraméterként használjuk, jelentősen egyszerűsödik a képletek alakja, ezért a szakirodalom jelentős része ezeket a formákat alkalmazza. A mélységélességet számtalan módon le lehet vezetni. Az oldalnagyítás a tárgytávolság és a gyújtótávolság függvénye. Ha e két utóbbi közül az egyiket kifejezzük és behelyettesítjük a már kidolgozott képletekbe, akkor más alakhoz jutunk. Természetesen ezek az eltérő eljárások, amennyiben helyesen járunk el, azonos eredményre vezetnek.
megjegyzés: egy későbbi anyagban a hiperfokális távolság gyakorlati jelentősége még alaposabb elemzésre kerül
A mélységélesség számítása megközelíthető a szóródási kör átmérőjének függvénye felől is, amely szintén felírható a fenti ábrákból. Attól függően, hogy az élesség síkja előtt vagy mögött járunk-e, más képletet kell alkalmaznunk. Mivel a függvény változója a tárgy vagy a képtávolság lehet, a már bevezetett (k0, t0) jelölés mellett a k, t – mint az aktuális tárgy és képtávolság jelölését is használnunk kell.
|
k = 1 / (1 / f – 1 / t) |
a leképzési törvény teremt kapcsolatot k és t között |
|
k0 = 1 / (1 / f – 1 / t0) |
ahogyan k0 és t0 között is |
|
CoC = (k – k0) / k * (f / f#) |
átmérő az élesre állított tárgy előtt… |
|
CoC = (k0 – k) / k0 * (f / f#) |
… és mögötte |
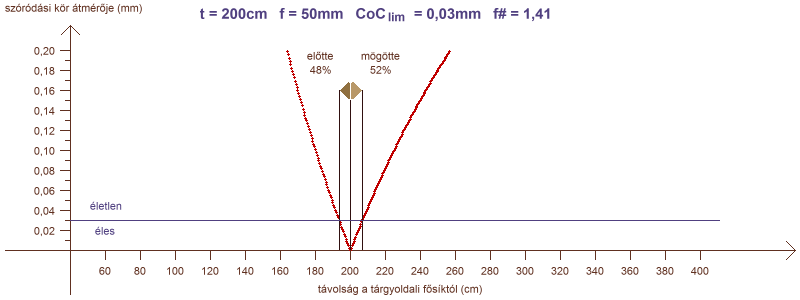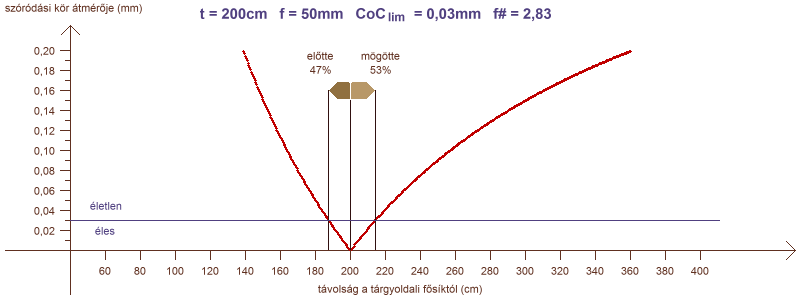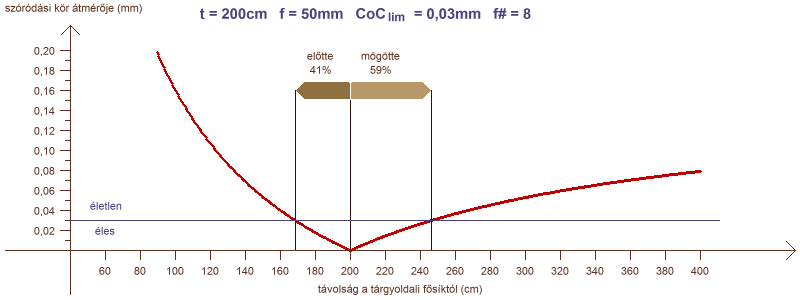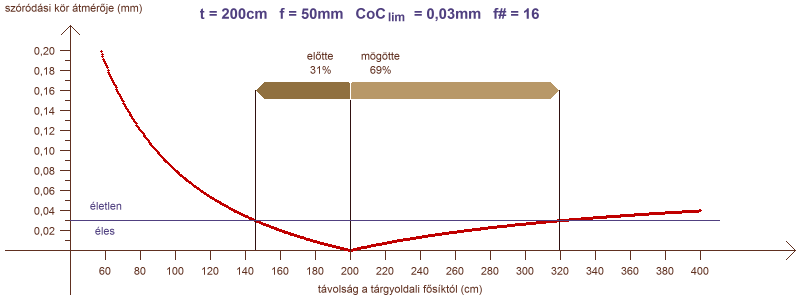
a szóródási kör átmérője a rekesszám függvényében
Az átmérőt mutató görbén látszik, hogy egy határozott értékhez tart. Ha ez az érték kisebb, mint a CoClim, akkor a távoli határ a végtelenben van, ezért a mélységélesség is végtelen. Ennek feltétele határérték-számítással a CoC (mögötte) függvényéből meghatározható.
A határok elemzése terén hátra van még egy olyan eset, amely igen gyakran merül fel kérdésként a fotósok között: hogyan alakul a mélységélesség, ha különböző gyújtótávolságú objektíveket alkalmazunk, de minden esetben azonosan töltjük ki az élesre állított témával a képet, tehát azonos az oldalnagyítás? Ezt a helyzetet mutatja a következő két ábra, ahol a vízszintes tengelyen a gyújtótávolság szerepel logaritmikus léptékben, és a hozzá tartozó tárgytávolság is fel van tüntetve, amely a kívánt oldalnagyítást garantálja:
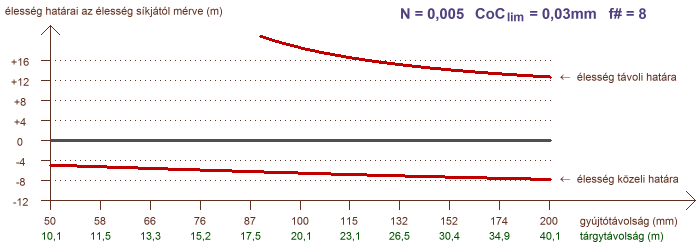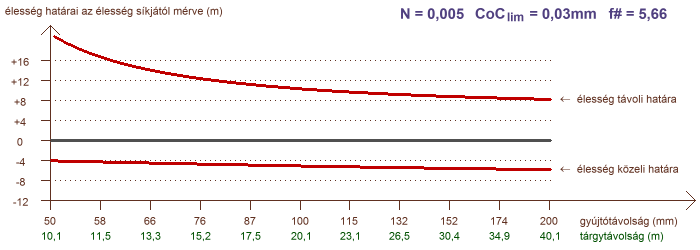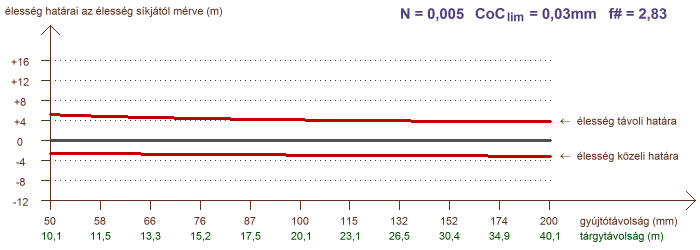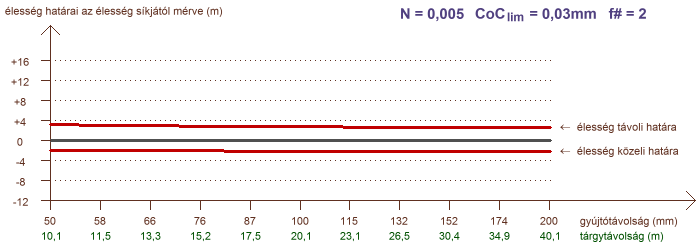
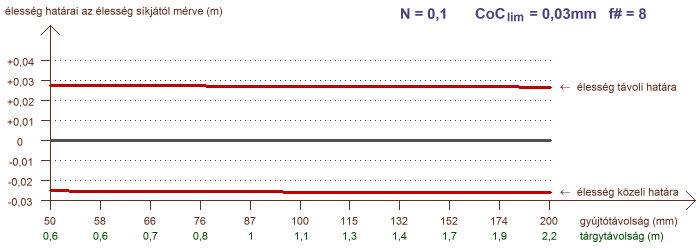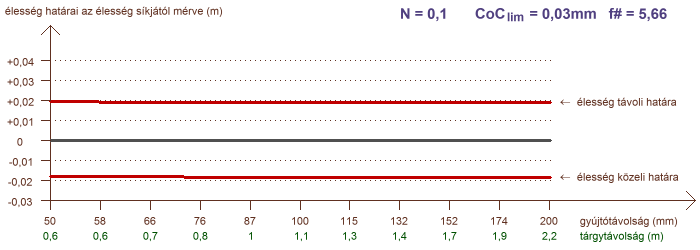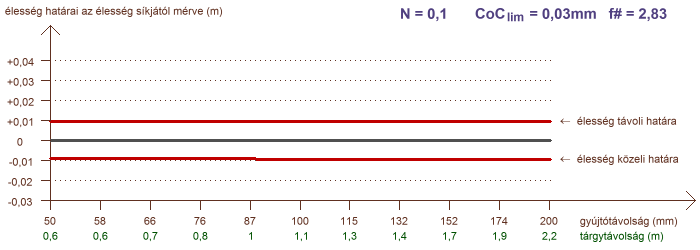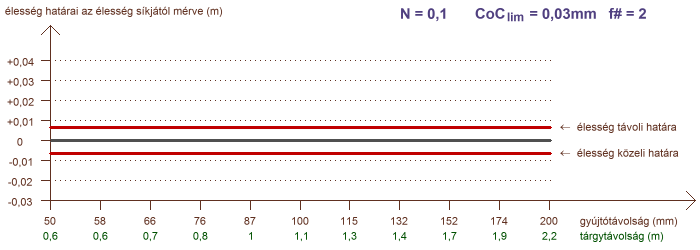
a mélységélesség N = 0,005 (1:200) és N = 0,1 (1:10) konstans oldalnagyítás esetére
A görbék azt mutatják, hogy ha az oldalnagyítás kis mértékű, akkor a mélységélesség függ az objektív gyújtótávolságától. Amennyiben a tárgytávolság egy nagyságrendbe esik a gyújtótávolsággal (a példában N = 0,1) a mélységélesség gyakorlatilag független a gyújtótávolságtól. Az is jól látszik, hogy az éles tartomány kiterjedésének aránya az élesség síkja előtt és mögött milyen feltételektől függ. Makrofényképezés, pl. 1:1 oldalnagyítás esetén a mélységélesség teljesen függetlenné válik a gyújtótávolságtól. A rekeszszám természetesen ilyenkor is jelentősen hatással bír.
Ezek a következtetések azonban nem jelentik azt, hogy a képi tartalom független lesz a gyújtótávolságtól egy állandó, nagy oldalnagyítás esetén. Fontos megérteni, hogy a mélységélesség függetlensége a CoClim kis értékének és annak köszönhető, hogy ilyen helyzetben a CoC-t leíró függvény az élesség síkja közelében szinte lineáris. A CoClim határt elhagyva a szóródási kör azonban teljesen más ütemben növekszik egy normálobjektív és egy teleobjektív esetében az élesség síkjától távolodva (továbbra is azonos oldalnagyításról van szó). A teleobjektív az élesre állított témánk mögötti, kissé távolabbi hátteret sokkal jobban elhomályosítja. Ez könnyen megérthető, ha a képszögre gondolunk. Bár a fő témával azonosan töltjük ki a képet, a beállított tárgytávolság kétszeresénél a teleobjektív már jóval kisebb szeletet vág ki a valóságból, mint a normálobjektív, jobban „széthúzva” azt, és ezáltal homályosabb lesz a háttér.
A tárgyalt modell és képlet helyzettől függően kisebb-nagyobb egyszerűsítéseket tartalmaz. A belépőpupilla mellett a kilépőpupilla is szerephez juthat. Míg előbbi az a látszólagos nyílás, amelyen keresztül a fény az objektívbe lép, utóbbi az a látszólagos nyílás, amelyen keresztül elhagyja azt. Ha feltételezzük, hogy az objektív szimmetrikus felépítésű, akkor a belépő- és kilépőpupilla azonos átmérőjű. Erősen aszimmetrikus objektíveknél, kis tárgytávolság esetén azonban eltérés jelentkezik a két méret között, így az un. pupillanagyítás jelentősége megnő. Eszerint kell módosítani a D = f / f# képletet, és a levezetést így folytatni.
Kísérlet
Ha a fenti képlet helyes, azt kísérlettel is igazolni lehet. A legegyszerűbb módszer, hogy a szóródási kör átmérőjét megmérjük különböző tárgytávolságok esetén, miközben az objektív élességállító mechanizmusát nem állítjuk el. Ehhez először tisztázni kell egy lényeges feltételt: nem célszerű alkalmazni belső élességállítású, lebegőtagos objektívet. Az ilyen eszközök gyújtótávolsága jelentősen változhat a beállított tárgytávolság függvényében, ezért egy régebbi, egyszerű felépítésű objektív jobban megfelel a kísérlethez. Azért is jobb ilyen objektívet használni, mert nagyobb esély van rá, hogy a fősíkok helyzetéről információra bukkanunk, illetve ha kísérlettel határozzuk meg, a pontatlanság nem okoz komoly mérési hibát, hiszen ezek az objektívek jóval kisebbek, mint a mai, általában sok lencséből álló társaik.
- objektív: Zuiko OM 50 mm 1:1.8
- tárgytávolság: 200 cm
- rekeszszám: f/4
- CoClim : 0,03 mm (a 35 mm-es filmre jellemzően használt érték)
- mérőeszköz: digitális fényképezőgép, 0,0055 × 0,0055 mm pixelméret
- teszt-fényforrás: kb. 0,26 mm átmérőjű fehéren világító pont, amely a 200 cm-hez tartozó oldalnagyításnál kb. 1,2 pixelt fed le
Ezekből az adatokból a képletek alapján a következő értékek adódnak:
- élesség közeli határa: 183 cm
- élesség távoli határa: 221 cm
- mélységélesség: 38 cm
- az éles tartomány élesség síkja elé eső résznek kiterjedése a mélységélességhez viszonyítva: 45%
- az éles tartomány élesség síkja mögé eső részének kiterjedése a mélységélességhez viszonyítva: 55%
A CoClim átmérőjéből és a mérőeszközünk pixelméretéből adódik, hogy 5,45 pixel átmérőjű lesz a szóródási kör az élesség határainál. Hogy ezt mekkorának látjuk majd a képen, a következő tényezők befolyásolják:
- az 5 egész feletti 0,45 pixel, ha halványabb árnyalattal is, de még a legszerencsésebb esetben is megjelenik
- a fényforrás átmérője nem végtelenül kicsi
- igen kis valószínűséggel esik pixelek határára a szóródási kör széle
- az objektív leképzése nem mentes a hibáktól (nem tökéletesen éles)
Ezek figyelembevételével a képen 6-7 pixelnyinek kell lennie a határon az értékelt átmérőnek. Pontosabb méréshez 2-3-szor kisebb pixelekkel rendelkező mérőeszközre lenne szükség. A CoClim követelményünket is lehetne növelni, ez is javítaná a pontosságot, azonban itt éppen ennek a kis átmérőnek van jelentősége (és még nehezebb lenne elemezni az egyre halványabb foltot, vagy minden felvételt másképpen kellene exponálni). A kísérletnek van azonban egy ennél sokkal fontosabb és biztatóbb eredménye: a szóródási kör átmérő-változásának trendje nagyon jól összevethető lesz a képletekkel, amely igazolhatja vagy cáfolhatja a bennük szereplő logikát.
Az alábbi képsorozat az elkészült felvételekből kivágott részleteket mutatja, sorba rendezve. A felvételek automata kontrasztbeállításon (és hamis színezésen) estek át, hogy a szóródási kör átmérőjének változása ne okozzon a képen látványos világosságkülönbséget. Az átmérő-változás nyomon követése érdekében egyfajta burkológörbeként fel van tűntetve a képlettel számolt átmérő is.

a mélységélesség-képlet ellenőrzése kísérlettel
Az ábrára tekintve megállapíthatjuk, hogy a CoC átmérőjének függvénye igen jól követi a felvételeken látható foltok méreteit, tehát az adott körülmények között a geometriai modell helyesnek bizonyult. A kísérletet elvégeztem 105 mm gyújtótávolságú objektívvel is, megegyező eredménnyel. A számított éles tartomány határainál a 6-7 pixel átmérőnek kell megjelennie:
| A kísérlet felvételei 800%-os nagyításban | ||
|---|---|---|
 |
 |
 |
| 3. | 12. | 13. |
 |
 |
 |
| 21. | 31. | 32. |
Bokeh
A bokeh műszó, amelyet egy magazin szerkesztője, Mike Johnston alkotott. Eredeti formájában ez egy „bo-ke” hangzású japán kifejezés, és homályosságot jelent. A bokeh-t a szóródási kör minőségének jellemzésére használják. Akkor jó minőségű a bokeh, ha az életlenül leképzett pontok a képen szabályos kör formájúak, és kontúrjaik nem erősek. Ilyenkor a kép életlen háttere szépen elmosódott, amelyre gyakran a „krémes” szót használják. A bokeh hatását akkor látjuk jól, ha erős, kis méretű fényforrások vannak az életlen (OOF = Out Of Focus azaz fókuszon kívüli) tartományban, pl. utcai lámpák, falevelek között átvilágító vagy vízfelületen tükröződő napfény. De általános esetben, pl. egy portrénál is ronthatnak a kép élvezeti értékén az összetett textúrákon megjelenő, szabálytalan, néha kettős kontúrokkal rendelkező foltok. Mivel a szóródási kör felveszi a belépőpupilla alakját, amelyet pedig a fényrekesz határoz meg, a fényrekesznek alapvető befolyása van a bokeh-re. A szép bokeh érdekében a drágább objektívekben sok lamellát használnak a fényrekeszben, a kis számú lamella ugyanis sokszögesíti a pupilla alakját. Fontos, hogy a lamellák a lehető legkevesebb fényt verjék vissza. Egyes szakirodalmak szerint a bokeh minőségét rontja, ha az objektív feloldóképessége sugár és érintőirányban jelentősen eltér (MTF görbe szétnyílik). A bokeh-t még tovább ronthatja az objektívek erős színi hibája (kromatikis aberráció). Ilyenkor a szóródási kör szélei színesedhetnek is, még zavarosabbá téve az életlen tartományt. A katadioptrikus tervezésű tükrös objektívek furcsa, gyűrűs szóródási köröket rajzolnak, amely miatt a fotósok sokszor elve elvetik alkalmazásukat. Közvetlenül az objektív elé helyezett, tetszőleges nyílású (pl. csillag, szív stb.) lappal bármilyen szóródási folt létrehozható, amellyel így különleges képhatást érhetünk el.


példa a gyengébb minőségű (balra) és a jó minőségű (jobbra) bokeh-re
Megjegyzések
A fotózás minden fogalmához kapcsolódnak félreértések, azonban a mélységélesség különleges helyen van e furcsa listában. A teljesség igénye nélkül csak azokat soroljuk itt fel, amelyek cáfolata hozzájárul a még jobb megértéshez.
A legnépszerűbb tévhit, hogy az élesnek tekintett tartományt az élesség síkja mindig 1/3:2/3 vagy egyéb rögzített arányban osztja fel. Az optikai geometria, a képletek és a kísérlet is nyilvánvalóan ellentmondanak ennek, de még csak nem is kell a szerkesztéshez nyúlni, hogy cáfolhassuk. Végtelenben lévő tárgyra fókuszáljunk úgy, hogy ne állítsuk az objektívet teljesen a végtelen állapotig, csak annyira, hogy a szóródási kör kisebb legyen, mint az elfogadott legnagyobb (a kihuzat csak kissé tér el a gyújtótávolságtól). A végtelentől már nem tudjuk távolabb vinni a tárgyat, a párhuzamos fénysugarak nem tudnak még párhuzamosabbak lenni, a szóródási kör már nem lesz nagyobb. Így az élesség síkja mögött minden élesnek tekinthető, a tárgy mögött végtelen, előtte véges lesz az éles tartomány. Tehát a rögzített arány elmélete képtálóból származtatott CoClim esetén bizonyítottan hamis. Ha belegondolunk ebbe a végtelen tárgytávolság közeli helyzetbe, még jobban megérhetjük, miért laposodik el, miért tart egy értékhez a CoC függvénye a távolban.
A másik nagyon gyakori félreértés, hogy a kisebb képméret nagyobb mélységélességet eredményez azonos objektívvel és beállításokkal. Ebben a formában azonban ez szintén hamis állítás. Kisebb képméret esetén a belőle számolt CoClim is kisebb lesz, így nem nő, hanem csökken a mélységélesség. Teljesen más azonban a helyzet, ha nem azonos gyújtótávolságú objektívre, hanem azonos képszögre (azonos egyenérték-gyújtótávolságú objektívre) számoljuk ki a mélységélességet, hiszen a valóságban is az ilyen helyzeteket hasonlítjuk egymáshoz. Az azonos képszög feltétele, hogy annyiszor kisebb legyen a gyújtótávolság, ahányszor kisebb a képméret. A kisebb gyújtótávolság viszont radikálisan növeli a mélységélességet (figyelem, itt nem azonos oldalnagyításról, hanem azonos tárgytávolságról beszélünk!). Ez a hatás jóval erősebb, mint a kisebb CoClim -ból származó mélységélesség-csökkenés, így végül növekedés lesz belőle. Tekintsünk a képletre, és látjuk, hogy a gyújtótávolság a négyzeten szerepel benne. Ezért a kompakt fényképezőgépekkel nehéz a hátteret és fő témát elválasztani egymástól a mélységélesség eszközeivel, de megfelelő optikai rendszer esetén könnyebb makrófelvételeket készíteni velük. Tehát a feltevés eredeti formájában nem igaz, csak ha az azonos gyújtótávolság helyére az azonos egyenérték-gyújtótávolság vagy képszög fogalmakat helyettesítjük.
Cserélhető objektíves fényképezőgépek esetén a telekonverterek alkalmazása is kérdéseket vet fel a mélységélességgel kapcsolatban. Egy objektív mögé helyezett optikai eszköz nem növelheti meg a belépőpupilla méretét, így ha a telekonverter növeli a gyújtótávolságot, a rekeszszám is változik, a fényerő csökken. Ennek köszönhető a telekonverterek által okozott fényveszteség is. Azonos körülmények között alkalmazva egy 200 mm 1:2,8 objektívet 2-szeres telekonverterrel és egy 400 mm 1:5,6 objektívet önmagában nem csak a szükséges expozíciós adatok fognak megegyezni, hanem a kialakuló mélységélesség is.
Az Interneten sok online vagy letölthető mélységélesség kalkulátor található. A rendkívül kis mélységélesség leginkább a makrofényképezésben jelentkezik problémaként. Sokan próbálják ezeket a programokat segítségül hívni, de a valóságban teljesen mást tapasztalnak, mint a számított értékek. Ez leginkább az előző részben tárgyalt problémából adódik. A kalkulátorok ugyanis az objektív pontos ismerete nélkül csak a tárgytávolságot kérdezhetik meg. A felhasználók viszont ebbe a mezőbe az élesreállítási távolságot írják be, tehát az érzékelő és a téma teljes távolságát, mivel ezt tudják lemérni. A gyártók által megadott „minimum focusing distance” is így mérendő. A tévedés a makrofényképezésben óriási, akár 100% feletti alapadat hibát jelent, hiszen le kellene vonni belőle a kihuzatot és a fősíkok távolságát (amely általában ismeretlen), így az eredmények teljesen használhatatlanok.
Az itt tárgyalt elmélet és kísérlet az általános fényképészeti helyzetekben elég jól megállják a helyüket. Ha azonban a tárgytávolság összemérhető az objektív gyújtótávolságával (1:10 oldalnagyítástól nagyobb érték) és az objektív korszerű, belső élességállítású, akkor annyi paraméter hiányzik, hogy nem fogunk pontos értéket kapni. Hiába bonyolítjuk a képleteket tökéletesre, ha újabb kísérletekkel tudjuk csak meghatározni a valós gyújtótávolságot és a fősíkok helyét, nem beszélve a pupillanagyításról. Ezért azt kell mondanom, hogy ilyen helyzetben a gyártók által kiadott mélységélesség táblázatokra kell hagyatkozni, vagy el kell végezni a fenti kísérletet otthon az adott objektívre, hiszen ez bárki által megtehető. Megfelelő fényforrást találni nagy oldalnagyítás esetén azonban nem lesz egyszerű, hiszen 1:1 -nél egy APS-C fényképezőgép esetén 0,02 mm a CoClim, amit ha csak (a kísérlethez hasonlóan) 5 pixelben mérünk, akkor 0,004 mm-nek kell a világító pontnak lennie.







